题目内容
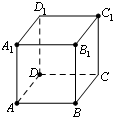
在棱长为1的正方体的表面上任取4个点构成一个三棱锥,则这个三棱锥体积的取值范围是( )
A.(0,
| B.(0,
| C.(0,
| D.(0,1) |

在正方体ABCD-A1B1C1D1中,设三棱锥的底面为α.
在正方体的表面上,离三棱锥底面α最远的点,一定可以在正方体的顶点处取得.此时,三棱锥的体积最大.固定住这个点,以这个点为三棱锥底面的一个点,则三棱锥的顶点一定可以在正方体的顶点处取得,同理,三棱锥体积最大时,三个顶点必在正方体的顶点处取得.
故正方体8个顶点中四个顶点形成三棱锥的体积最大的那个即为所求.
由于三棱锥四个顶点不共面,故在面ABCD和面A1B1C1D1中,分别可能有三棱锥的(1,3),(2,2),(3,1)个顶点,其中(1,3)和(3,1)是对称的.
故只需讨论(3,1)和(2,2)的情形.
若为(3,1),在底面,不妨取A、B、D顶点可为A1、B1、C1、D1,三棱锥体积都为V=
•S△ABD•h=
×
×1×1×1=
,
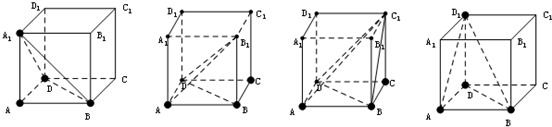
若为(2,2)
则在底面可取A、B或A、C.
若为A、B,顶面可取(A1,C1),(A1,D1),三棱锥体积V=
S•h=
.
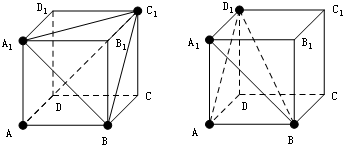
若为A、C,则顶点可取B1D1此时
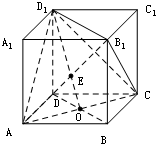 VD-ACD1=VD1-ACD∴
VD-ACD1=VD1-ACD∴
×
×
2•h=
×
×1×1×1∴h=
∴hB1-ACD1=B1D-h=
V=
S△ACD1•hB1-ACD1=
•
•(
)2
=
故选B.
在正方体的表面上,离三棱锥底面α最远的点,一定可以在正方体的顶点处取得.此时,三棱锥的体积最大.固定住这个点,以这个点为三棱锥底面的一个点,则三棱锥的顶点一定可以在正方体的顶点处取得,同理,三棱锥体积最大时,三个顶点必在正方体的顶点处取得.
故正方体8个顶点中四个顶点形成三棱锥的体积最大的那个即为所求.
由于三棱锥四个顶点不共面,故在面ABCD和面A1B1C1D1中,分别可能有三棱锥的(1,3),(2,2),(3,1)个顶点,其中(1,3)和(3,1)是对称的.
故只需讨论(3,1)和(2,2)的情形.
若为(3,1),在底面,不妨取A、B、D顶点可为A1、B1、C1、D1,三棱锥体积都为V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |

若为(2,2)
则在底面可取A、B或A、C.
若为A、B,顶面可取(A1,C1),(A1,D1),三棱锥体积V=
| 1 |
| 3 |
| 1 |
| 6 |

若为A、C,则顶点可取B1D1此时
 VD-ACD1=VD1-ACD∴
VD-ACD1=VD1-ACD∴| 1 |
| 3 |
| ||
| 4 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 2 |
2
| ||
| 3 |
| 1 |
| 3 |
故选B.

练习册系列答案
相关题目
 的面对角线
的面对角线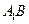 上存在
上存在 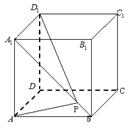 一点
一点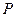 使得
使得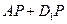 取得最小值,则此最小值为
取得最小值,则此最小值为