题目内容

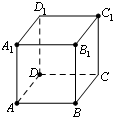
已知正方体ABCD-A1B1C1D1，则三棱锥D1-AB1C的体积与正方体ABCD-A1B1C1D1的体积之比为（　　）
A．1：3B．1：4C．1：2D．1：6
设正方体ABCD-A1B1C1D1的棱长为1，
则正方体ABCD-A1B1C1D1的体积V2=1，
三棱锥D1-AB1C为各棱长均为
2
的正四面体
底面面积S=
3
2
，高为
2
3
3

故三棱锥D1-AB1C的体积V1=
1
3
×
3
2
×
2
3
3
=
1
3

故三棱锥D1-AB1C的体积与正方体ABCD-A1B1C1D1的体积之比V1：V2=1：3
故选：A
练习册系列答案
相关题目
半径为
3
的球内有一个内接正三棱锥P-ABC，过球心O及一侧棱PA作截面截三棱锥及球面，所得截面如右图所示，则此三棱锥的侧面积为______．
在圆锥PO中，已知PO=2
2
，⊙O的直径AB=4，点C在底面圆周上，且∠CAB=30°，D为AC的中点．
（1）证明：AC⊥平面POD；
（2）求点O到面PAD的距离．
已知四棱锥P-ABCD的体积为V，AB∥CD，且AB：CD=2：3，点Q是PA的中点，则三棱锥Q-PBC的体积是（　　）
A．
V
5
B．
2V
5
C．
3V
5
D．
3V
10
在棱长为1的正方体的表面上任取4个点构成一个三棱锥，则这个三棱锥体积的取值范围是（　　）
A．（0，
1
6
]		B．（0，
1
3
]		C．（0，
1
2
]		D．（0，1）
正方体ABCD-A1B1C1D1中，O是上底面ABCD中心，若棱长为a，则三棱锥O-AB1D1的体积为______．
正四面体的四个顶点都在一个球面上，且正四面体的高为4，则球的表面积为（　　）
A．16(12-6
3
)π		B．18πC．36πD．64(6-4
2
)π
在正方体ABCD-A1B1C1D1中，已知AC=2
6
，则这个正方体内切球的体积为（　　）
A．12πB．9πC．4
3
π		D．4π
如图，空间四边形ABCD中，E，F，G，H分别是直线AB，BC，CD，DA上的点，如果EF∩GH=Q，则点Q在直线（　　）上．
A．BDB．ABC．ACD．CD

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网