题目内容
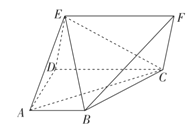
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点M.设
相交于点M.设![]() ,
,![]() .
.

(1)试用向量![]() 表示
表示![]() .
.
(2)在线段![]() 上取点E,在线段
上取点E,在线段![]() 取点F,使
取点F,使![]() 过点M.设
过点M.设![]() ,
,![]() ,其中
,其中![]() 当
当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() ;当
;当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() .能否由此得出般结论:不论
.能否由此得出般结论:不论![]() 在线段
在线段![]() 上如何变动,等式
上如何变动,等式![]() 恒成立,请说明理由.
恒成立,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)设![]() ,根据
,根据![]() 三点共线,得
三点共线,得![]() 一个等量关系;再根据
一个等量关系;再根据![]() 三点共线,得
三点共线,得![]() 另一个等量关系,最后解方程组即得结果;
另一个等量关系,最后解方程组即得结果;
(2)根据![]() 三点共线,得
三点共线,得![]() ,再根据平面向量基本定理得
,再根据平面向量基本定理得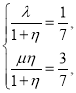 ,最后消去
,最后消去![]() 即得结论.
即得结论.
(1)不妨设![]() ,一方面由
,一方面由![]() 三点共线,可知存在
三点共线,可知存在![]() (
(![]() ,且
,且![]() )使得
)使得![]() ,则
,则![]() ,于是
,于是![]() .
.
又![]() ,所以
,所以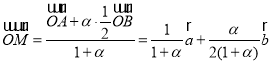 ,从而
,从而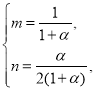 即
即![]() ①.另一方面由
①.另一方面由![]() 三点共线,可知存在
三点共线,可知存在![]() (
(![]() 且
且![]() )使得
)使得![]() ,则
,则![]() ,于是
,于是![]() .
.
又![]() ,
,
所以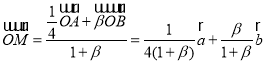 ,
,
从而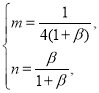 即
即![]() ②.
②.
由①②可得![]() ,
,![]() .
.
故![]() .
.
(2)可以得出结论.理由:
由于![]() 三点共线,所以存在实数
三点共线,所以存在实数![]() (
(![]() 且
且![]() )使得
)使得![]() ,于是
,于是![]() .
.
又![]() ,
,![]() ,
,
所以![]() ,
,
于是![]() ,
,
从而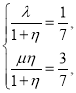 消去
消去![]() 即得
即得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】(题文)随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”的赞成人数如下表:
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“使用微信交流”的态度与人的年龄有关.
列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“使用微信交流”的态度与人的年龄有关.
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成的人数 | |||
不赞成的人数 | |||
合计 |
(2)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考公式:![]() ,
,![]() .
.
参考数据:
| 0.100 |
|
|
|
|
|
|
|
|