题目内容
【题目】在一个风雨交加的夜里,某水库闸房(设为A)到某指挥部(设为B)的电话线路有一处发生了故障.这是一条
长的线路,想要尽快地查出故障所在.如果沿着线路一小段小段地查找,困难很多,每查一小段需要很长时间.
(1)维修线路的工人师傅随身带着话机,他应怎样工作,才能每查一次,就把待查的线路长度缩减一半?
(2)要把故障可能发生的范围缩小到
,最多要查多少次?
【答案】（1）见解析（2）7次
【解析】
（1）运用“二分法”的原理进行查找，即可得出结论．
（2）二分法求方程的近似解的定义和方法，由
且
，求得
的最小值，从而得出结论．
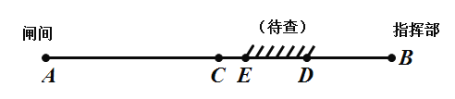
解:(1)如图所示,他首先从中点C查,用随身带的话机向两端测试时,假设发现
段正常,可断定故障在
段,再到段中点D查,这次若发现
段正常,可断定故障在
段,再到段中点E来查,依次类推即可.
(2)每一次二等分，区间长度变为原来的
，由 且，
解得
，
故每查一次,可以把待查的线路长度缩减一半,因此最多查
次就够了.
阅读快车系列答案
【题目】某高三年级在一次理科综合检测中统计了部分“住校生”和“非住校生”共20人的物理、化学的成绩制成下列散点图（物理成绩用
表示，化学成绩用
表示）（图1）和生物成绩的茎叶图（图2）.
（图1）
住校生 非住校生
2 6
9 8 5 4 4 3 1 7 4 5 7 7 9 9
6 5 8 2 2 5 7
（图2）
（1）若物理成绩高于90分，我们视为“优秀”，那么以这20人为样本，从物理成绩优秀的人中随机抽取2人，求至少有1人是住校生的概率；
（2）若化学成绩高于80分，我们视为“优秀”，根据图1完成如下列联表，并判断是否有95%的把握认为优秀率与住校有关；
住校 | 非住校 | |
优 秀 | ||
非优秀 |
附：（
,其中
）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（3）若生物成绩高于75分，我们视为“良好”，将频率视为概率，若从全年级学生中任选3人，记3人中生物成绩为“良好”的学生人数为随机变量
，求出的分布列和数学期望.
