题目内容
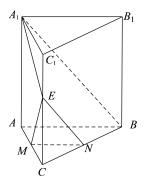
【题目】已知五面体ABCDEF中,四边形CDEF为矩形,![]() ,CD=2DE=2AD=2AB=4,AC=
,CD=2DE=2AD=2AB=4,AC=![]() ,
,![]() .
.
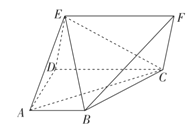
(1)求证:AB![]() 平面ADE;
平面ADE;
(2)求平面EBC与平面BCF所成的锐二面角的余弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据勾股定理得![]() ,再根据线面垂直判定定理得结果,(2)先根据条件证得直线DE,DA,DC两两互相垂直,再建立空间直角坐标系,设立各点坐标,利用方程组解得平面EBC和平面BCF法向量,利用向量数量积得法向量夹角,最后根据二面角与向量夹角关系得结果.
,再根据线面垂直判定定理得结果,(2)先根据条件证得直线DE,DA,DC两两互相垂直,再建立空间直角坐标系,设立各点坐标,利用方程组解得平面EBC和平面BCF法向量,利用向量数量积得法向量夹角,最后根据二面角与向量夹角关系得结果.
(1)因为![]() ,
,![]() ,所以
,所以![]()
因为四边形CDEF为矩形,所以![]() ,
,
因为![]()
![]() ,
,![]() 所以
所以![]() ,
,
因为![]() ,所以
,所以![]()
(2)因为 ![]() ,
,![]() ,所以
,所以![]() ,
,![]()
由(1)得![]() ,所以直线DE,DA,DC两两互相垂直,
,所以直线DE,DA,DC两两互相垂直,
故以点D为坐标原点,分别以![]() 正方向为
正方向为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
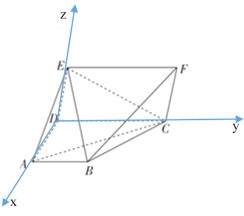
则E(0,0,2)A(2,0,0),C(0,4,0),B(2,2,0),F(0,4,2)![]() ,
,
设平面EBC和平面BCF法向量分别为![]() ,
,![]() ,
,
则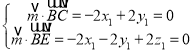 ,所以
,所以![]() ,
,
取![]() 得
得![]() ,
,
同理,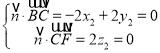 所以
所以![]()
取![]() 得
得![]()
设所求角为![]() ,则
,则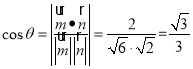 ,即所求锐二面角的余弦值为
,即所求锐二面角的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值
为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了100件这种产品,
配方)做实验,各生产了100件这种产品,
并测量了每件产品的质量指标值,得到下面的试验结果:(以下均视频率为概率)
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
![]() 配方的频数分配表
配方的频数分配表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 40 | 30 |
(Ⅰ)若从![]() 配方产品中有放回地随机抽取3件,记“抽出的
配方产品中有放回地随机抽取3件,记“抽出的![]() 配方产品中至少1件二级品”为事件
配方产品中至少1件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(Ⅱ)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: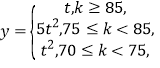 其中
其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?