题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,使得
,使得![]() (
(![]() ),求实数
),求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时, ![]() 有极小值,极小值为
有极小值,极小值为![]() ,无极大值;(Ⅱ)
,无极大值;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极值即可;
(Ⅱ)得到![]() , 设
, 设![]() 在
在![]() 上的值域为A,函数
上的值域为A,函数![]() 在
在![]() 上的值域为B,根据函数的单调性求出m的范围即可
上的值域为B,根据函数的单调性求出m的范围即可
试题解析:
(Ⅰ)依题意, ![]() ,
,
![]() ,
,
因为![]() ,故当
,故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
故当![]() 时,
时, ![]() 有极小值,极小值为
有极小值,极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)当![]() =1时,
=1时, ![]()
因为![]() ,
, ![]() ,使得
,使得![]() ,
,
故![]() ;设
;设![]() 在
在![]() 上的值域为A,
上的值域为A,
函数![]() 在
在![]() 上的值域为B,
上的值域为B,
当![]() 时,
时, ![]() ,即函数
,即函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,又
,又![]() .
.
(i)当![]() 时,
时, ![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() 的值域为
的值域为![]() ,
,
因为![]() ,又
,又![]() ,故
,故![]() ,即
,即![]() ;
;
(ii)当![]() 时,
时, ![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() 的值域为
的值域为![]() ,因为
,因为![]() ,又
,又![]() ,
,
故![]() ,故
,故![]() ;
;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
污染 |
污染 |
污染 |
|
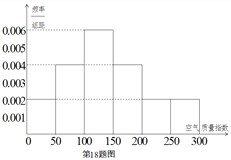
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.