题目内容
【题目】已知函数f（x）=|x|+|x+1|．
（1）解关于x的不等式f（x）＞3；
（2）若x∈R，使得m2+3m+2f（x）≥0成立，试求实数m的取值范围．
【答案】
（1）解：由|x|+|x+1|＞3，
得： 
或 
或 
，
解得：x＞1或x＜﹣2，
故不等式的解集是{x|x＞1或x＜﹣2}
（2）解：若x∈R，使得m2+3m+2f（x）≥0成立，
而f（x）= 
，故f（x）的最小值是1，
故只需m2+3m+2≥0即可，
解得：m≥﹣1或m≤﹣2
【解析】（1）通过讨论x的范围，得到关于x的不等式组，解出即可；（2）求出f（x）的最小值，问题转化为m2+3m+2≥0，解出即可．
【考点精析】关于本题考查的绝对值不等式的解法，需要了解含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能得出正确答案．
全优点练单元计划系列答案
【题目】“大众创业，万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号．某生产企业积极响应号召，大力研发新产品，为了对新研发的一批产品进行合理定价，将该产品按事先拟定的价格进行试销，得到一组销售数据（xi ， yi）（i=1，2，…，6），如表所示：
试销单价x（元） | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y（件） | q | 84 | 83 | 80 | 75 | 68 |
已知 
=80．
（Ⅰ）求出q的值；
（Ⅱ）已知变量x，y具有线性相关关系，求产品销量y（件）关于试销单价x（元）的线性回归方程 
；可供选择的数据： 
， 
（Ⅲ）用 
表示用（Ⅱ）中所求的线性回归方程得到的与xi对应的产品销量的估计值．当销售数据（xi ， yi）对应的残差的绝对值 
时，则将销售数据（xi ， yi）称为一个“好数据”．现从6个销售数据中任取3个，求“好数据”个数ξ的分布列和数学期望E（ξ）．
（参考公式：线性回归方程中 
， 
的最小二乘估计分别为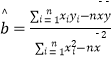 
， 
）
