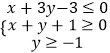题目内容
【题目】已知抛物线E:![]() 的焦点为F,过点F的直线l与E交于A,C两点
的焦点为F,过点F的直线l与E交于A,C两点
(1)分别过A,C两点作抛物线E的切线,求证:抛物线E在A、C两点处的切线互相垂直;
(2)过点F作直线l的垂线与抛物线E交于B,D两点,求四边形ABCD的面积的最小值.
【答案】(1)见解析;(2)32
【解析】
(1)设出直线l的方程与抛物线联立,利用韦达定理及导数求得斜率相乘为﹣1即可;
(2)用弦长公式求出弦长|AC|和|BD|,再算出面积后,用基本不等式求最值.
(1)证明:设过点F(0,1)的直线方程为:y=kx+1,
由![]() ,得x2﹣4kx﹣4=0,
,得x2﹣4kx﹣4=0,
设A(x1,y1),C(x2,y2),
则![]() ,
,
∵y![]() x2,∴y′
x2,∴y′![]() x,
x,
设抛物线E在点A、C两点处的切线的斜率分别为k1,k2,
则k1k2![]() x1
x1![]() x2
x2![]() x1x2=﹣1,
x1x2=﹣1,
故抛物线E在A,C两点处的切线互相垂直.
(2)由(1)知|AC|![]() 4(k2+1)
4(k2+1)
同理|BD|=4(![]() 1)
1)
∴S四边形ABCD![]() |AC||BD|=8(k2+1)(1
|AC||BD|=8(k2+1)(1![]() )
)
=8(1+k2![]() 1)
1)
≥8(2+2![]() )
)
=32,
∴四边形ABCD的面积的最小值为32.

练习册系列答案
相关题目