题目内容
【题目】某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地,图中DE需把基地分成面积相等的两部分,D在AB上,E在AC上. 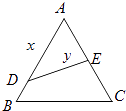
(1)设AD=x(x≥10),ED=y,试用x表示y的函数关系式;
(2)如果DE是灌溉输水管道的位置,为了节约,则希望它最短,DE的位置应该在哪里?如果DE是参观线路,则希望它最长,DE的位置又应该在哪里?说明理由.
【答案】
(1)解:∵△ABC的边长是20米,D在AB上,则10≤x≤20,
S△ADE= ![]() S△ABC,
S△ABC,
∴ ![]() xAEsin60°=
xAEsin60°= ![]()
![]() (20)2,
(20)2,
故AE= ![]() ,
,
在三角形ADE中,由余弦定理得:
y= ![]() ,(10≤x≤20);
,(10≤x≤20);
(2)解:若DE作为输水管道,则需求y的最小值,
∴y= ![]() ≥
≥ ![]() =10
=10 ![]() ,
,
当且仅当x2= ![]() 即x=10
即x=10 ![]() 时“=”成立.
时“=”成立.
【解析】(1)三角形ADE中的∠A=60°,由余弦定理得y,x,AE三者的关系求出函数的解析式即可;(2)根据基本不等式的性质求出函数的最小值即可.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
