题目内容
19.在极坐标系中,已知点P的极坐标为(4,$\frac{π}{3}$).(1)若极点不变,将极轴顺时针旋转$\frac{π}{6}$,求点P在新坐标系中的极坐标;
(2)将极点已知O′(2$\sqrt{3}$,$\frac{π}{6}$)处,极轴方向不变,求点P在新坐标系中的极坐标.
分析 (1)由题意可得则点P在新坐标系中极径不变,极角比原来增大$\frac{π}{6}$,由此可得点P在新坐标系中的极坐标.
(2)(2)将极点已知O′(2$\sqrt{3}$,$\frac{π}{6}$)处,极轴方向不变,数形结合求得OP的值以及∠x′O′P的值,可得点P在新坐标系下的极坐标.
解答 解:(1)已知点P的极坐标为(4,$\frac{π}{3}$),若极点不变,将极轴顺时针旋转$\frac{π}{6}$,
则点P在新坐标系中极径不变,极角比原来增大$\frac{π}{6}$,故点P在新坐标系中的极坐标为(4,$\frac{π}{2}$).
(2)将极点已知O′(2$\sqrt{3}$,$\frac{π}{6}$)处,极轴方向不变,如图所示:A是OP直线和x′轴的交点,
则由题意可得OP=4,OO′=2$\sqrt{3}$,∠xOO′=$\frac{π}{6}$=∠OO′A,∠xOP=$\frac{π}{3}$,
利用余弦定理求得O′P=$\sqrt{{OP}^{2}{+OO′}^{2}-2OP•OO′cos∠O′OP}$=$\sqrt{16+12-2•4•2\sqrt{3}•\frac{\sqrt{3}}{2}}$=2,
∴OP2+O′P2=OO′2,∴∠PO′O=$\frac{π}{2}$,∴∠PO′A=∠PO′O-∠OO′A=$\frac{π}{2}$-$\frac{π}{6}$=$\frac{π}{3}$,
∴点P在新坐标系下的辐角主值为∠x′O′P=π-∠PO′A=$\frac{2π}{3}$,
故点P在新坐标系下的极坐标为(2,$\frac{2π}{3}$).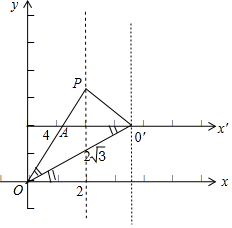
点评 本题主要考查点的极坐标和直角坐标的互化,坐标系的平移,体现了转化、数形结合的数学思想,属于基础题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案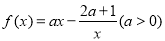 ,若
,若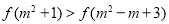 ,则实数
,则实数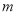 的取值范围是( )
的取值范围是( )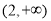 B.
B.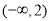
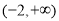 D.
D.