题目内容
7.(x2+x-$\frac{1}{x}$)6的展开式中的常数项是-5.分析 把原式后两项组合展开二项式定理,然后求出每一项中的常数项作和得答案.
解答 解:由(x2+x-$\frac{1}{x}$)6=$[{x}^{2}+(x-\frac{1}{x})]^{6}$
=${C}_{6}^{0}({x}^{2})^{6}(x-\frac{1}{x})^{0}+{C}_{6}^{1}({x}^{2})^{5}(x-\frac{1}{x})$$+{C}_{6}^{2}({x}^{2})^{4}(x-\frac{1}{x})^{2}+{C}_{6}^{3}({x}^{2})^{3}(x-\frac{1}{x})^{3}$$+{C}_{6}^{4}({x}^{2})^{2}(x-\frac{1}{x})^{4}+{C}_{6}^{5}({x}^{2})^{1}(x-\frac{1}{x})^{5}$$+{C}_{6}^{6}({x}^{2})^{0}(x-\frac{1}{x})^{6}$.
∵$(x-\frac{1}{x})^{4}$中含有x-4的项为${C}_{4}^{4}{x}^{0}(-\frac{1}{x})^{4}={x}^{-4}$,
$(x-\frac{1}{x})^{5}$中含有x-2的项不存在,
$(x-\frac{1}{x})^{6}$中的常数项为${C}_{6}^{3}{x}^{3}(-\frac{1}{x})^{3}=-{C}_{6}^{3}$.
∴(x2+x-$\frac{1}{x}$)6的展开式中的常数项是${C}_{6}^{4}-{C}_{6}^{3}=-5$.
故答案为:-5.
点评 本题考查了二项式系数的性质,考查了分析问题和解决问题的能力,考查了计算能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,且
,且 .
. 在区间
在区间 上单调递增;
上单调递增; ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.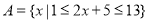 ,
,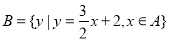 ,则
,则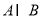 等于( )
等于( )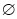 B.
B.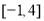
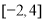 D.
D.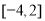

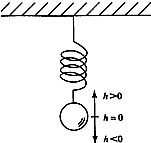 如图,弹簧挂着的小球上下振动,时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost,t∈[0,+∞).,则小球开始振动时h的值为$\sqrt{2}$,小球振动时最大的高度差为4.
如图,弹簧挂着的小球上下振动,时间t(s)与小球相对于平衡位置(即静止时的位置)的高度h(cm)之间的函数关系式是h=$\sqrt{2}$sint+$\sqrt{2}$cost,t∈[0,+∞).,则小球开始振动时h的值为$\sqrt{2}$,小球振动时最大的高度差为4.