题目内容
2.设数列{an}(n=1,2,3…)的前n项和Sn,满足Sn=2an-a1,且a1,a2+1,a3成等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列$\left\{{\frac{1}{a_n}}\right\}$的前n项和为Tn,求Tn.
分析 (Ⅰ)由条件Sn满足Sn=2an-a1,求得数列{an}为等比数列,且公比q=2;再根据a1,a2+1,a3成等差数列,求得首项的值,可得数列{an}的通项公式.
(Ⅱ)由于$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n}}$,利用等比数列的前n项和公式求得数列$\left\{{\frac{1}{a_n}}\right\}$的前n项和Tn.
解答 解:(Ⅰ)由已知Sn=2an-a1,有
an=Sn-Sn-1=2an-2an-1(n≥2),
即an=2an-1(n≥2),
从而a2=2a1,a3=2a2=4a1.
又因为a1,a2+1,a3成等差数列,即a1+a3=2(a2+1)
所以a1+4a1=2(2a1+1),
解得:a1=2.
所以,数列{an}是首项为2,公比为2的等比数列.
故an=2n.
(Ⅱ)由(Ⅰ)得$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n}}$,
所以Tn=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$.
点评 本题主要考查数列的前n项和与第n项的关系,等差、等比数列的定义和性质,等比数列的前n项和公式,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
17.已知函数f(x)=$\frac{1}{x+2}$-k|x|({k∈R})有三个不同的零点,则实数k的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |

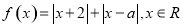 .
.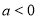 ,且
,且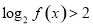 对任意
对任意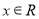 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且关于
,且关于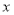 的不等式
的不等式 有解,求实数
有解,求实数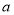 的取值范围.
的取值范围.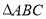 中,角
中,角 所对的边分别为
所对的边分别为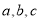 ,且
,且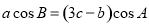 .
. ,求
,求 ;
; ,且
,且 的面积为
的面积为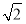 ,求
,求 的周长.
的周长. ,且
,且 .
. 在区间
在区间 上单调递增;
上单调递增; ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.