题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则x3(1x+x2)+$\frac{1}{{{x}_{3}}^{2}{x}_{4}}$的取值范围是(-1,1].
分析 作出函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$的图象,由图象可得x1+x2=-2,x3x4=1;1<x4≤2;从而化简x3(1x+x2)+$\frac{1}{{{x}_{3}}^{2}{x}_{4}}$,再利用函数的单调性求出它的取值范围.
解答  解:作出函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$的图象,
解:作出函数f(x)=$\left\{\begin{array}{l}{|x+1|,x≤0}\\{|lo{g}_{2}x|,x>0}\end{array}\right.$的图象,
∵方程f(x)=a有四个不同的解x1,x2,x3,x4,
且x1<x2<x3<x4,
由图可知a<1,x1+x2=-2.
∵-log2(x3)=log2(x4)=a,∴x3x4=1;
∵0<log2(x4)<1,∴1<x4≤2.
故x3(x1+x2)+$\frac{1}{{{x}_{3}}^{2}{x}_{4}}$=-$\frac{2}{{x}_{4}}$+x4,
其在1<x4≤2上是增函数,
故-2+1<-$\frac{2}{{x}_{4}}$+x4≤-1+2;
即-1<-$\frac{2}{{x}_{4}}$+x4≤1;
故答案为:(-1,1].
点评 本题主要考查分段函数的应用,函数零点与方程的根的关系,体现了数形结合、转化的数学思想,属于中档题.

练习册系列答案
相关题目
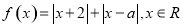 .
.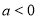 ,且
,且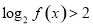 对任意
对任意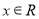 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且关于
,且关于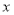 的不等式
的不等式 有解,求实数
有解,求实数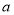 的取值范围.
的取值范围.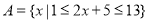 ,
,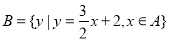 ,则
,则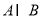 等于( )
等于( )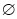 B.
B.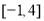
 D.
D.