题目内容
17.已知i为虚数单位,且z=i(1-i),则复数z的共轭复数为( )| A. | -1+i | B. | 1-i | C. | 1+i | D. | -1-i |
分析 先化简z,然后根据共轭复数的定义进行求解即可.
解答 解:∵z=i(1-i)=1+i,
∴复数z的共轭复数为1-i,
故选:B
点评 本题主要考查共轭复数的求解,比较基础.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
8.由直线x-y+1=0,x+y-5=0和x-1=0所围成的三角形区域(包括边界)用不等式组可表示为( )
| A. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
2.已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=1024,则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值为( )
| A. | 21 | B. | 35 | C. | 56 | D. | 210 |
9.复数$\frac{2+i}{i}$(i为虚数单位)在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
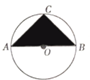 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.