题目内容
11.设命题p:?x∈R,x2+x+1<0;命题q:?x∈[1,2],x2-1≥0;则以下命题是真命题的是( )| A. | ¬p∧¬q | B. | p∨¬q | C. | ¬p∧q | D. | p∧q |
分析 先判断命题p、q的真假性,再判断复合命题的真假性即可.
解答 解:∵?x∈R,x2+x+1=${(x+\frac{1}{2})}^{2}$+$\frac{3}{4}$>0,
∴命题p是假命题;
又∵x∈[1,2]时,x2-1≥0恒成立,
∴命题q是真命题;
对于A,¬p为真命题,¬q为假命题,∴¬p∧¬q是假命题:
对于B,p为假命题,¬q为假命题,∴p∨¬q是假命题;
对于C,¬p是真命题,q是真命题,∴¬p∧q是真命题;
对于D,p是假命题,q是真命题,∴p∧q是假命题.
故选:C.
点评 本题考查了复合命题的真假性判断问题,解题时应熟记复合命题的真值表,是基础题目.

练习册系列答案
相关题目
6.下列四个命题中,真命题是( )
| A. | a>b,c>d⇒ac>bd | B. | a<b⇒a2<b2 | C. | $\frac{1}{a}<\frac{1}{b}$⇒a>b | D. | a>b,c<d⇒a-c>b-d |
20.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=2$\overrightarrow{DB}$,则$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$其中m,n分别为( )
| A. | m=$\frac{1}{3}$,n=-$\frac{2}{3}$ | B. | m=$\frac{1}{3}$,n=$\frac{2}{3}$ | C. | m=-$\frac{2}{3}$,n=$\frac{1}{3}$ | D. | m=$\frac{2}{3}$,n=$\frac{1}{3}$ |
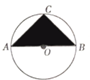 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.