题目内容
13．设函数f（x）=sinx+cosx，把f（x）的图象向右平移m（m＞0）个单位长度后图象恰好为函数g（x）=sinx-cosx的图象，则m的最小值为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |
分析 化简两个函数的表达式为正弦函数的形式，按照平移的方法平移，即可得到m的最小值．
解答 解：∵函数f（x）=sinx+cosx=$\sqrt{2}$sin（x+$\frac{π}{4}$），g（x）=sinx-cosx=$\sqrt{2}$sin（x-$\frac{π}{4}$），
所以函数f（x）至少向右平移$\frac{π}{2}$个单位，可得f（x-$\frac{π}{2}$）=$\sqrt{2}$sin（x-$\frac{π}{2}$+$\frac{π}{4}$）=$\sqrt{2}$sin（x-$\frac{π}{4}$）=g（x），
即m的最小值为：$\frac{π}{2}$．
故选：C．
点评 本题考查两角和的正弦函数以及三角函数图象的平移，考查计算能力，属于基础题．
练习册系列答案
相关题目
3．α，β，γ为平面，l是直线，已知α∩β=l，则“α⊥γ，β⊥γ”是“l⊥γ”的（ ）条件．
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分不必要条件 |
1．
已知平行四边形ABCD中，点E为CD的中点，$\overrightarrow{AM}$=m•$\overrightarrow{AB}$，$\overrightarrow{AN}$=n$\overrightarrow{AD}$（m•n≠0），若$\overrightarrow{MN}$∥$\overrightarrow{BE}$，则$\frac{n}{m}$等于（ ）
已知平行四边形ABCD中，点E为CD的中点，$\overrightarrow{AM}$=m•$\overrightarrow{AB}$，$\overrightarrow{AN}$=n$\overrightarrow{AD}$（m•n≠0），若$\overrightarrow{MN}$∥$\overrightarrow{BE}$，则$\frac{n}{m}$等于（ ）| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | -2 |
8．由直线x-y+1=0，x+y-5=0和x-1=0所围成的三角形区域（包括边界）用不等式组可表示为（ ）
| A． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≤0}\\{x≥1}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-5≥0}\\{x≤1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-y+1≤0}\\{x+y-5≤0}\\{x≤1}\end{array}\right.$ |
18．下列结论正确的是（ ）
| A． | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$，则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B． | 已知向量$\overrightarrow{a}$，$\overrightarrow{b}$为非零向量，则“$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$•$\overrightarrow{b}$＜0” | |
| C． | 若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0 | |
| D． | “若θ=$\frac{π}{3}$，则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$，则cosθ$≠\frac{1}{2}$” |
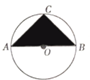如图，等腰直角△ABC内接于以AB为直径的圆O，假设你在圆形上随机撒一粒黄豆，则黄豆落到阴影部分的概率为$\frac{1}{π}$．