题目内容
10.设Sn是公差不为0的等差数列{an}的前n项和,S3=a22,且S1,S2,S4成等比数列,则a10=( )| A. | 15 | B. | 19 | C. | 21 | D. | 30 |
分析 由S3=a22,结合等差数列的求和公式可求a2,然后由${{S}_{2}}^{2}={S}_{1}•{S}_{4}$,结合等差数列的求和公式进而可求公差d,结合通项公式进行求解即可.
解答 解:设数列的公差为d,(d≠0)
∵S3=a22,得:3${a}_{2}={{a}_{2}}^{2}$,
∴a2=0或a2=3;
∵S1,S2,S4成等比数列,
∴${{S}_{2}}^{2}={S}_{1}•{S}_{4}$,
∴$(2{a}_{2}-d)^{2}=({a}_{2}-d)(4{a}_{2}+2d)$,
若a2=0,则可得d2=-2d2即d=0不符合题意,
若a2=3,则可得(6-d)2=(3-d)(12+2d),
解可得d=0(舍)或d=2,
∴a10=a2+8d=3+8×2=3+16=19,
故选:B.
点评 本题主要考查了等差数列的通项公式及求和公式的应用,等比数列的性质的简单应用,利用方程组思想是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 已知平行四边形ABCD中,点E为CD的中点,$\overrightarrow{AM}$=m•$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AD}$(m•n≠0),若$\overrightarrow{MN}$∥$\overrightarrow{BE}$,则$\frac{n}{m}$等于( )
已知平行四边形ABCD中,点E为CD的中点,$\overrightarrow{AM}$=m•$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AD}$(m•n≠0),若$\overrightarrow{MN}$∥$\overrightarrow{BE}$,则$\frac{n}{m}$等于( )
 已知平行四边形ABCD中,点E为CD的中点,$\overrightarrow{AM}$=m•$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AD}$(m•n≠0),若$\overrightarrow{MN}$∥$\overrightarrow{BE}$,则$\frac{n}{m}$等于( )
已知平行四边形ABCD中,点E为CD的中点,$\overrightarrow{AM}$=m•$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AD}$(m•n≠0),若$\overrightarrow{MN}$∥$\overrightarrow{BE}$,则$\frac{n}{m}$等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
18.下列结论正确的是( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$为非零向量,则“$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$•$\overrightarrow{b}$<0” | |
| C. | 若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1>0 | |
| D. | “若θ=$\frac{π}{3}$,则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$,则cosθ$≠\frac{1}{2}$” |
2.已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=1024,则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值为( )
| A. | 21 | B. | 35 | C. | 56 | D. | 210 |
19.直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( )
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
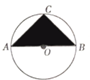 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.