题目内容
14.甲、乙两人分别从四种不同品牌的商品中选择两种,则甲、乙所选的商品中恰有一种品牌相同的选法种数是( )| A. | 30 | B. | 24 | C. | 12 | D. | 6 |
分析 根据题意,分2步进行分析:①、甲乙在四种不同品牌的商品中选择一种,②、在剩下的三种品牌中,任取2种,再分配给甲乙2人,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、甲乙在四种不同品牌的商品中选择一种,有C41=4种,
②、在剩下的三种品牌中,任取2种,再分配给甲乙2人,有A32=6种情况,
则甲、乙所选的商品中恰有一种品牌相同的选法种数是4×6=24种;
故选:B.
点评 本题考查排列、组合的运用,解题的关键是根据题设中的问题对问题正确分布讨论,再利用计数原理求得答案.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
2.已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=1024,则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值为( )
| A. | 21 | B. | 35 | C. | 56 | D. | 210 |
9.复数$\frac{2+i}{i}$(i为虚数单位)在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为( )
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
20.在△ABC中,已知D是AB边上一点,若$\overrightarrow{AD}$=2$\overrightarrow{DB}$,则$\overrightarrow{CD}$=m$\overrightarrow{CA}$+n$\overrightarrow{CB}$其中m,n分别为( )
| A. | m=$\frac{1}{3}$,n=-$\frac{2}{3}$ | B. | m=$\frac{1}{3}$,n=$\frac{2}{3}$ | C. | m=-$\frac{2}{3}$,n=$\frac{1}{3}$ | D. | m=$\frac{2}{3}$,n=$\frac{1}{3}$ |
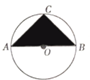 如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.
如图,等腰直角△ABC内接于以AB为直径的圆O,假设你在圆形上随机撒一粒黄豆,则黄豆落到阴影部分的概率为$\frac{1}{π}$.