题目内容
9．直线$\sqrt{3}$x-y-1=0的倾斜角为$\frac{π}{3}$．分析 求出直线的斜率，根据斜率和倾斜角的关系进行求解．
解答 解：直线的斜击式方程为y=$\sqrt{3}$x-1，
则斜率k=$\sqrt{3}$，由tanα=$\sqrt{3}$，
解得α=$\frac{π}{3}$，
故倾斜角α=$\frac{π}{3}$，
故答案为：$\frac{π}{3}$
点评 本题主要考查直线倾斜角的求解，根据直线斜率和倾斜角的关系是解决本题的关键．
练习册系列答案
相关题目
19．双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1的渐近线方程是（ ）
| A． | y=±$\sqrt{2}$x | B． | y=±$\frac{{\sqrt{2}}}{2}$x | C． | y=±$\frac{1}{2}$x | D． | y=±2x |
20．下列函数f（x）中，满足“对任意x1，x2∈（0，+∞），当x1＜x2时，都有f（x1）＞f（x2）”的是（ ）
| A． | f（x）=$\frac{1}{x}$ | B． | f（x）=x+$\frac{1}{x}$ | C． | f（x）=（x-1）2 | D． | f（x）=ln（x+1） |
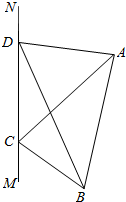如图，为对某失事客轮AB进行有效援助，现分别在河岸MN选择两处C、D用强光柱进行辅助照明，其中A、B、C、D在同一平面内．现测得CD长为100米，∠ADN=105°，∠BDM=30°，∠ACN=45°，∠BCM=60°．
18．在曲线y=x3上切线的斜率为3的点是（ ）
| A． | （0，0） | B． | （1，1） | C． | （-1，-1） | D． | （1，1）或（-1，-1） |