题目内容
19.双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1的渐近线方程是( )| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |
分析 直接利用双曲线方程求渐近线方程即可.
解答 解:双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1可得$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{2}=0$,所以双曲线的渐近线方程为:y=±$\frac{{\sqrt{2}}}{2}$x.
故选:B.
点评 本题考查双曲线的渐近线方程的求法,基本知识的考查.

练习册系列答案
相关题目
9. 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
14.在(1+x)6(2+y)4的展开式中,含x4y3项的系数为( )
| A. | 210 | B. | 120 | C. | 80 | D. | 60 |
4.(x-2y)7的展开式中的第4项为( )
| A. | -35x4y3 | B. | 280x4y3 | C. | -280x4y3 | D. | 35x4y3 |
11.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
附:${Χ^2}=\frac{{n({n_{11}}{n_{22}}-{n_{12}}{n_{21}})2}}{{{n_{11}}{n_{21}}{n_{12}}{n_{22}}}}$
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
8.某程序框图如图所示,则该程序运行后输出的值是 ( )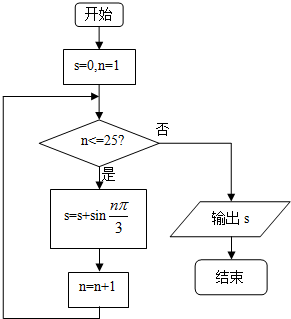

| A. | -$\sqrt{3}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1-\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |