题目内容
3.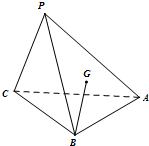 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.(1)试判断直线BG与AC的位置关系,并说明理由;
(2)记H为AB中点,当PA=$\sqrt{5}$时,求直线HG与平面PAC所成角的正弦值.
分析 (1)根据异面直线判定定理,可得直线BG与AC异面;
(2)以O原坐标原点,建立空间坐标系,求出直线HG的方向向量和平面PAC的法向量,代入向量夹角公式,可得直线HG与平面PAC所成角的正弦值.
解答 解:(1)直线BG与AC异面,理由如下:
延长BG交PA于D,如下图所示:
由PA?平面PAC,可得D∈平面PAC,
即BG∩平面PAC=D,
又由AC?平面PAC,D∉AC,
可得:直线BG与AC异面;
(2)如图所示,取BC的中点O,连接OA,OP,
∵PB=PC,
∴OP⊥BC.
∵AB=AC=2$\sqrt{2}$,∠BAC=90°,PB=PC=$\sqrt{5}$,
∴BC=4,OA=OB=OC=$\frac{1}{2}BC$=2,OP=$\sqrt{P{B}^{2}{-OB}^{2}}$=1,
又由PA=$\sqrt{5}$,可得:OA2+OP2=PA2,即OP⊥OA,
∵OA∩BC=O,OA,BC?平面ABC,
∴OP⊥平面ABC,
∴OA,OB,OP两两互相垂直
以O原坐标原点,建立如图所示的空间直角坐标系,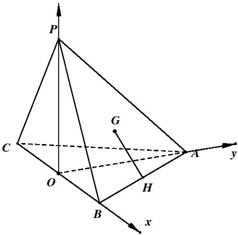
则B(2,0,0),A(0,2,0),C(-2,0,0),P(0,0,1),H(1,1,0),
∵G为△PAB的重心,
∴G($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$),
∴$\overrightarrow{HG}$=(-$\frac{1}{3}$,-$\frac{1}{3}$,$\frac{1}{3}$),$\overrightarrow{AC}$=(-2,-2,0),$\overrightarrow{PA}$=(0,2,-1),
设平面PAC的一个法向量是$\overrightarrow{m}$=(x,y,z),则由:
$\left\{\begin{array}{l}\overrightarrow{m}•\overrightarrow{AC}=0\\ \overrightarrow{m}•\overrightarrow{PA}=0\end{array}\right.$得:$\left\{\begin{array}{l}-2x-2y=0\\ 2y-z=0\end{array}\right.$,
令x=-1,则$\overrightarrow{m}$=(-1,1,2),
记直线HG与平面PAC所成角为θ,
则sinθ=$\frac{|\overrightarrow{m}•\overrightarrow{HG}|}{\left|\overrightarrow{m}\right|•\left|\overrightarrow{HG}\right|}$=$\frac{\sqrt{2}}{3}$,
故直线HG与平面PAC所成角的正弦值为$\frac{\sqrt{2}}{3}$.
点评 本题主要考查了直线与平面之间所成角,异面直线的判定,考查空间想象能力、运算能力和推理论证能力,属于中档题

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案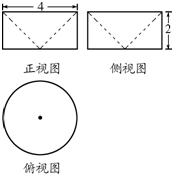
| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | $\frac{5}{8}$ |
| A. | 4$\sqrt{2}$ | B. | 3+$\sqrt{5}$ | C. | 2$\sqrt{2}$+1 | D. | 3+2$\sqrt{2}$ |
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$). 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,PA=$\sqrt{6}$,M为PC的中点.