题目内容
8.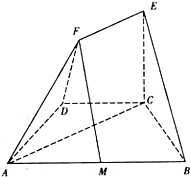 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.(I)求证:FM∥平面BCE;
(Ⅱ)若EC⊥平面ABCD,求证:BC⊥AF.
分析 (I)取BC的中点N,连结MN,EN.先证明出四边形MNEF为平行四边形,推断出FM∥EN,进而利用线面平行的判定定理证明出FM∥平面BCE.
(Ⅱ)先证明出ABCD为等腰梯形.推断出∠CMB=∠CBM=60°,判断出△CMB为等边三角形,推断出CM=MB=$\frac{1}{2}$AB.进而证明出△ABC为直角三角形,即BC⊥AC.最后利用线面垂直的判定定理证明出BC⊥面ACEF,则BC⊥AF得证.
解答 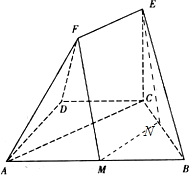 (I)证明:取BC的中点N,连结MN,EN.
(I)证明:取BC的中点N,连结MN,EN.
在△ABC中,MN∥AC,MN=$\frac{1}{2}$AC.
又∵EF∥AC,EF=$\frac{1}{2}$AC,
∴EF∥MN,EF=MN,
∴四边形MNEF为平行四边形,
∴FM∥EN,
∵FM?平面BCE,EN?平面BCE,
∴FM∥平面BCE.
(Ⅱ)证明:由(I)知AD∥MC,
∴∠DAM=∠CMB=60°,
∴ABCD为等腰梯形.
∴∠CBM=∠DAM=60°,∠CMB=∠CBM=60°,
∴△CMB为等边三角形,
∴CM=MB=$\frac{1}{2}$AB.
∴△ABC为直角三角形,即BC⊥AC.
又∵EC⊥面ABCD,BC?面ABCD,
∴EC⊥BC.
又∵EC与AC相交,且同在平面ACEF内,
∴BC⊥面ACEF,
∵AF?面ACEF,
∴AF⊥BC.
点评 本题主要考查了线面平行和线面垂直的判定定理的运用.注重了对学生空间观察能力和基础定理的灵活运用的考查.

练习册系列答案
相关题目
17.某班的一次数学考试后,按学号统计前20名同学的考试成绩如茎叶图所示,则该样本数据的中位数为( )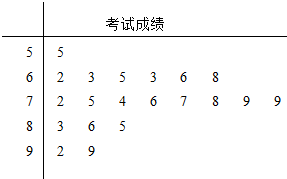

| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
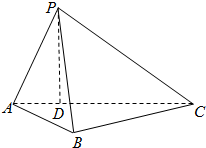 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.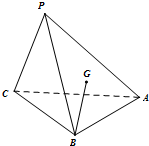 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.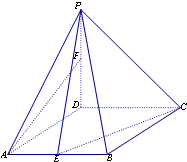 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.