题目内容
11.已知等腰直角三角形ABC的腰长AC=1,底角A的角平分线交对边BC于点D,则$\overrightarrow{AD}•\overrightarrow{BC}$=1-$\sqrt{2}$.分析 先建立平面直角坐标系,表示出C,A,B的坐标,再根据底角A的角平分线交对边BC于点D,设∠DAB=∠θ,和二倍角公式求出tanθ=$\sqrt{2}$-1,继而求出D的坐标,根据向量的坐标运算即可求出$\overrightarrow{AD}•\overrightarrow{BC}$=1-$\sqrt{2}$,
解答  解:以定点C为坐标原点,以AC所在的直线为x轴,以BC所在的直线为y轴,
解:以定点C为坐标原点,以AC所在的直线为x轴,以BC所在的直线为y轴,
则C(0,0),A(1,0),B(0,1),
∵底角A的角平分线交对边BC于点D,设∠DAB=∠θ,
∴θ=22.5°,
∵tan45=$\frac{2tanθ}{1-ta{n}^{2}θ}$=1,
∴tanθ=$\sqrt{2}$-1,
∴CD=ACtanθ=$\sqrt{2}$-1,
∴D(0,$\sqrt{2}$-1),
∴$\overrightarrow{AD}$=(-1,$\sqrt{2}$-1),$\overrightarrow{BC}$=(0,-1),
∴$\overrightarrow{AD}•\overrightarrow{BC}$=1-$\sqrt{2}$,
故答案为:1-$\sqrt{2}$
点评 本题考查了向量的坐标运算和三角函数的化简和求值,本题的关键的建立平面直角坐标系,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
5.执行如图程序框图其输出结果是( )


| A. | 29 | B. | 31 | C. | 33 | D. | 35 |
 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.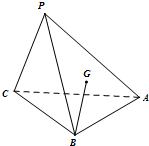 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心. 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.