题目内容
17．已知某几何体的三视图如图所示，则该几何体的体积为（ ）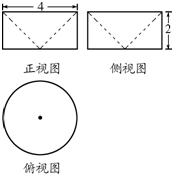
| A． | $\frac{8}{3}$π | B． | $\frac{16}{3}$π | C． | 8π | D． | 16π |
分析 由已知中的三视图，可知该几何体是一个圆柱挖去一个同底等高的圆锥，分别计算柱体和圆锥的体积，相减可得答案．
解答 解：由已知中的三视图，可知该几何体是一个圆柱挖去一个同底等高的圆锥，
圆柱和圆锥的底面直径为4，故底面半径为2，故底面面积S=4π，
圆柱和圆锥的高h=2，
故组合体的体积V=（1-$\frac{1}{3}$）Sh=$\frac{16}{3}π$，
故选：B
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
7．已知数列{an}满足a1=3，且an+1=an+log3（1+$\frac{1}{n}$），则a9=（ ）
| A． | 3 | B． | 4 | C． | log310+3 | D． | 5 |
8．
如图一个倒三角形数表：
它的排列规则是：第i（i=2，…，101）行的第j（j=1，2，…，102-i）个数ai．j=$\frac{{a}_{i-1，j}+{a}_{i-1，j+1}}{2}$，现设a1．j=xj-1（j=1，2，…，101），其中x＞0，若a101.1=$\frac{1}{{2}^{50}}$，则x=（ ）
如图一个倒三角形数表：它的排列规则是：第i（i=2，…，101）行的第j（j=1，2，…，102-i）个数ai．j=$\frac{{a}_{i-1，j}+{a}_{i-1，j+1}}{2}$，现设a1．j=xj-1（j=1，2，…，101），其中x＞0，若a101.1=$\frac{1}{{2}^{50}}$，则x=（ ）
| A． | $\sqrt{2}$-1 | B． | 1-$\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
5．执行如图程序框图其输出结果是（ ）
| A． | 29 | B． | 31 | C． | 33 | D． | 35 |
12．“a≥3”是“?x∈[1，2]，使得x2-a≤0”的（ ）
| A． | 充要条件 | B． | 必要不充分条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
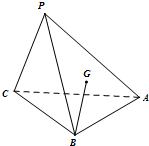点P是△ABC所在的平面外一点P，连结PA、PB、PC，且有PB=PC=$\sqrt{5}$，AB=AC=2$\sqrt{2}$，∠BAC=90°，G为△PAB的重心．