题目内容
14. 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象如图所示,则函数y=f(x)的解析式是y=2sin(2x+$\frac{π}{6}$).
分析 由已知中函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象,结合最值求出A,结合周期求出ω,结合特殊点的坐标求出φ,可得答案.
解答 解:由已知中函数y=Asin(ωx+φ)(A>0,ω>0,|φ|$<\frac{1}{2}$)的一段图象,
由最大值为2,可得A=2,
由T=$\frac{11π}{12}-(-\frac{π}{12})$=π,
可得ω=$\frac{2π}{T}$=2,
又由第一点坐标为$(-\frac{π}{12},0)$点,
故2×($-\frac{π}{12}$)+φ=2kπ,k∈Z,
即φ=2kπ+$\frac{π}{6}$,k∈Z,
当k=0时,φ=$\frac{π}{6}$,满足条件,
故y=2sin(2x+$\frac{π}{6}$)
故答案为:y=2sin(2x+$\frac{π}{6}$)
点评 本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,熟练掌握参数A,ω,φ的求法是解答的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
8. 如图一个倒三角形数表:
如图一个倒三角形数表:
它的排列规则是:第i(i=2,…,101)行的第j(j=1,2,…,102-i)个数ai.j=$\frac{{a}_{i-1,j}+{a}_{i-1,j+1}}{2}$,现设a1.j=xj-1(j=1,2,…,101),其中x>0,若a101.1=$\frac{1}{{2}^{50}}$,则x=( )
 如图一个倒三角形数表:
如图一个倒三角形数表:它的排列规则是:第i(i=2,…,101)行的第j(j=1,2,…,102-i)个数ai.j=$\frac{{a}_{i-1,j}+{a}_{i-1,j+1}}{2}$,现设a1.j=xj-1(j=1,2,…,101),其中x>0,若a101.1=$\frac{1}{{2}^{50}}$,则x=( )
| A. | $\sqrt{2}$-1 | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
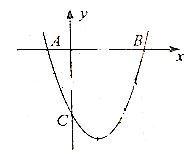 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.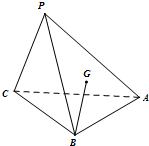 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.