题目内容
【题目】已知圆C过点A(1,4),B(3,2),且圆心在x轴上,求圆C的方程.
【答案】解法一:设圆C:(x﹣a)2+y2=r2 , 则 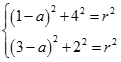
解得 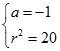 所以圆C的方程为(x+1)2+y2=20.
所以圆C的方程为(x+1)2+y2=20.
解法二:设圆C:x2+y2+Dx+F=0,
则 ![]()
解得 ![]() 所以圆C的方程为x2+y2+2x﹣19=0.
所以圆C的方程为x2+y2+2x﹣19=0.
解法三:因为圆C过两点A(1,4),B(3,2),所以圆心C必在线段AB的垂直平分线l上,
又因为 ![]() ,所以kl=1,又AB的中点为(2,3),
,所以kl=1,又AB的中点为(2,3),
故AB的垂直平分线l的方程为y﹣3=x﹣2,即y=x+1.
又圆心C在x轴上,所以圆心C的坐标为(﹣1,0),
所以半径 ![]() ,
,
所以圆C的方程为(x+1)2+y2=20
【解析】法一:设圆C:(x﹣a)2+y2=r2 , 利用待定系数法能求出圆C的方程.法二:设圆C:x2+y2+Dx+F=0,利用待定系数法能求出圆C的方程. 法三:由已知圆心C必在线段AB的垂直平分线l上,AB的中点为(2,3),由此能求出圆心C的坐标和半径,从而能求出圆C的方程.

练习册系列答案
相关题目