题目内容

在数列{an}中，a1=1，an+1•
an
=8
（Ⅰ）求a2，a3；
（Ⅱ）设bn=log2an，求证：{bn-2}为等比数列；
（Ⅲ）求{an}的前n项积Tn．
（Ⅰ）∵a2•
a1
=8，a1=1，
∴a2=8．
∵a3•
a2
=8，a1=8，
∴a3=2
2
．
（Ⅱ）证明：∵
bn+1-2
bn-2
=
log2an+1-2
log2an-2

=
log2
8
an
-2
log2an-2
=
3-
1
2
log2an-2
log2an-2

═
1
2
×
2-log2an
log2an-2
=-
1
2
．
∴{bn-2}为等比数列，首项为b1-2，即为-2，其公比为-
1
2
．
（Ⅲ）设数列{bn-2}的前n项和为Sn
Sn=
-2(1-(-
1
2
)n)
1+
1
2
=b1+b2+b3+…+bn-2n=log2a1+log2a2+…log2an-2n
=log2Tn-2n
．
∴log2Tn=
4
3
[(-
1
2
)n-1]+2n，
∴Tn=2
4
3
[(-
1
2
)n-1]+2n．
练习册系列答案
相关题目
设数列{an}的前n项和为Sn，且Sn=4an+2n+1，n∈N*．
（1）求证：{an-2}是等比数列；
（2）求数列{nan}前n项和Tn．
已知等差数列前三项为a，4，3a，前n项的和为sn，sk=2550．
（1）求a及k的值；
（2）求
1
s1
+
1
s2
+…+
1
sn
．
已知数列{an}满足Sn=n2an（n∈N*），其中Sn是{an}的前n项和，且a1=1，求
（1）求an的表达式；
（2）求Sn．
已知函数f（x）满足f（x+1）=3f（x）+2，若a1=1，an=f（n）．
（1）设Cn=an+1，证明：{Cn}是等比数列；
（2）设Sn是数列{an}的前n项和，求Sn．
已知无穷数列{an}的前n项和为Sn，且满足Sn=A
a2n
+Ban+C，其中A、B、C是常数．
（1）若A=0，B=3，C=-2，求数列{an}的通项公式；
（2）若A=1，B=
1
2
，C=
1
16
，且an＞0，求数列{an}的前n项和Sn；
（3）试探究A、B、C满足什么条件时，数列{an}是公比不为-1的等比数列．
在数列1，2，2，3，3，3，4，4，4，4， 中，第25项为       。
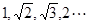数列的一个通项公式为         ．
记数列{an}的前n项和为Sn，且Sn=2（an-1），则a2=（　　）
A．4B．2C．1D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网