题目内容
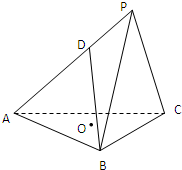
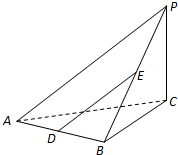
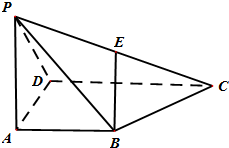
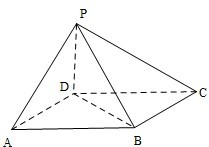
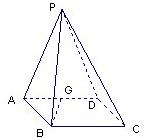
如图在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求二面角A-BC-P的大小.
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求二面角A-BC-P的大小.

(1)证明:
∵△PAD为正三角形,G为AD边的中点,∴PG⊥AD,
∵平面PAD垂直于底面ABCD,∴PG⊥底面ABCD,∴PG⊥BG
在菱形ABCD中,∠DAB=60°,AB=a
∴BG2=a2+
a2-2a•
a•cos60°=
a2,
∴△ABG为直角三角形,
且BG⊥AG,PG∩AD=G,∴BG⊥平面PAD
(2)由(1)知PG⊥底面ABCD,BG⊥AD,AD∥BC,
∴BG⊥BC,PB⊥BC,
∴∠PBG是二面角A-BC-P的平面角,
∵PG=
a,BG=
a,∴tan∠PBG=1,∴∠PBG=
∵△PAD为正三角形,G为AD边的中点,∴PG⊥AD,
∵平面PAD垂直于底面ABCD,∴PG⊥底面ABCD,∴PG⊥BG
在菱形ABCD中,∠DAB=60°,AB=a
∴BG2=a2+
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∴△ABG为直角三角形,
且BG⊥AG,PG∩AD=G,∴BG⊥平面PAD
(2)由(1)知PG⊥底面ABCD,BG⊥AD,AD∥BC,
∴BG⊥BC,PB⊥BC,
∴∠PBG是二面角A-BC-P的平面角,
∵PG=
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目