题目内容
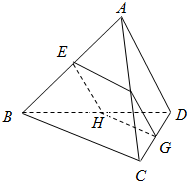
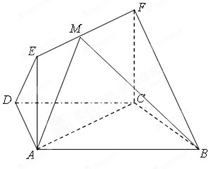
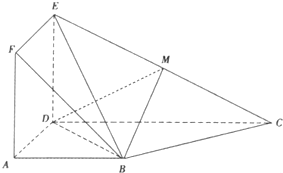
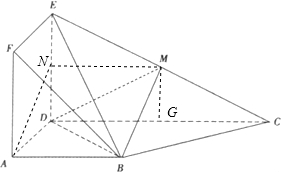
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=1,CD=2,DE=4,M为CE的中点.
(Ⅰ)求证:BM∥平面ADEF:
(Ⅱ)求证:BC⊥平面BDE;
(Ⅲ)求三棱锥C-MBD的体积.
(Ⅰ)求证:BM∥平面ADEF:
(Ⅱ)求证:BC⊥平面BDE;
(Ⅲ)求三棱锥C-MBD的体积.

(I)证明:取DE中点N,连接MN,AN
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
CD.
由已知AB∥CD,AB=
CD,所以MN∥AB,且MN=AB.
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,且BM?平面ADEF,
所以BM∥平面ADEF;
(II)证明:在矩形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
在△BCD中,BD=BC=
,CD=2,
因为BD2+BC2=CD2,所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE,
(Ⅲ)取CD中点G,连接MG,则MG∥DE且MG=
DE=2
∵ED⊥平面ABCD
∴MG⊥平面ABCD
∵BC⊥DB且BC=BD=
∴VC-MBD=VM-BCD=
S△BCD×MG=
×
×
×
×2=
.
在△EDC中,M、N分别为EC,ED的中点,所以MN∥CD,且MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
所以四边形ABMN为平行四边形,所以BM∥AN
又因为AN?平面ADEF,且BM?平面ADEF,
所以BM∥平面ADEF;

(II)证明:在矩形ADEF中,ED⊥AD,
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
因为BD2+BC2=CD2,所以BC⊥BD.
因为BD∩DE=D,所以BC⊥平面BDE,
(Ⅲ)取CD中点G,连接MG,则MG∥DE且MG=
| 1 |
| 2 |
∵ED⊥平面ABCD
∴MG⊥平面ABCD
∵BC⊥DB且BC=BD=
| 2 |
∴VC-MBD=VM-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目