题目内容
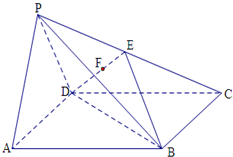
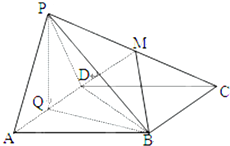
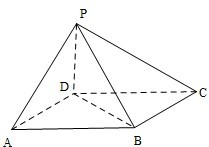
如图,四棱锥P-ABCD中,底面ABCD为平行四边形.∠DAB=60°,AB=2AD,PD⊥底面
ABCD.
(Ⅰ)证明:PA⊥BD
(Ⅱ)设PD=AD=1,求棱锥D-PBC的高.
ABCD.
(Ⅰ)证明:PA⊥BD
(Ⅱ)设PD=AD=1,求棱锥D-PBC的高.

(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=
AD,
从而BD2+AD2=AB2,故BD⊥AD
又PD⊥底面ABCD,可得BD⊥PD
所以BD⊥平面PAD.故PA⊥BD.
(II)作DE⊥PB于E,已知PD⊥底面ABCD,
则PD⊥BC,由(I)知,BD⊥AD,又BC∥AD,
∴BC⊥BD.
故BC⊥平面PBD,BC⊥DE,
则DE⊥平面PBC.
由题设知PD=1,则BD=
,PB=2.
根据DE•PB=PD•BD,得DE=
,
即棱锥D-PBC的高为
.
| 3 |
从而BD2+AD2=AB2,故BD⊥AD
又PD⊥底面ABCD,可得BD⊥PD
所以BD⊥平面PAD.故PA⊥BD.
(II)作DE⊥PB于E,已知PD⊥底面ABCD,
则PD⊥BC,由(I)知,BD⊥AD,又BC∥AD,
∴BC⊥BD.
故BC⊥平面PBD,BC⊥DE,
则DE⊥平面PBC.
由题设知PD=1,则BD=
| 3 |
根据DE•PB=PD•BD,得DE=
| ||
| 2 |
即棱锥D-PBC的高为
| ||
| 2 |

练习册系列答案
相关题目