题目内容
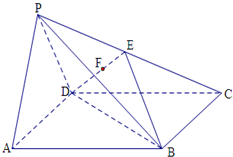
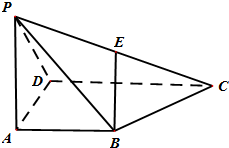
如图，四棱锥P-ABCD的底面ABCD为直角梯形，其中BA⊥AD，CD⊥AD，CD=AD=2AB，PA⊥底面ABCD，E是PC的中点．
（1）求证：BE∥平面PAD；
（2）若AP=2AB，求证：BE⊥CD．
（1）求证：BE∥平面PAD；
（2）若AP=2AB，求证：BE⊥CD．
（1）证明：如图，；
取CD的中点M，连接EM、BM，则四边形ABMD为矩形，
∴EM∥PD，BM∥AD；
又∵BM∩EM=M，
∴平面EBM∥平面APD；
而BE?平面EBM，
∴BE∥平面PAD；
（2）如图，
；
取PD的中点F，连接FE，
则FE∥DC，BE∥AF，
又∵DC⊥AD，DC⊥PA，
∴DC⊥平面PAD，
∴DC⊥AF，DC⊥PD，
∴EF⊥AF，
在Rt△PAD中，∵AD=AP，F为PD的中点，
∴AF⊥PD，又AF⊥EF且PD∩EF=F，
∴AF⊥平面PDC，又BE∥AF，
∴BE⊥平面PDC．
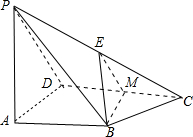
取CD的中点M，连接EM、BM，则四边形ABMD为矩形，
∴EM∥PD，BM∥AD；
又∵BM∩EM=M，
∴平面EBM∥平面APD；
而BE?平面EBM，
∴BE∥平面PAD；
（2）如图，
；取PD的中点F，连接FE，
则FE∥DC，BE∥AF，
又∵DC⊥AD，DC⊥PA，
∴DC⊥平面PAD，
∴DC⊥AF，DC⊥PD，
∴EF⊥AF，
在Rt△PAD中，∵AD=AP，F为PD的中点，
∴AF⊥PD，又AF⊥EF且PD∩EF=F，
∴AF⊥平面PDC，又BE∥AF，
∴BE⊥平面PDC．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
