Question

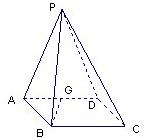
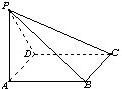
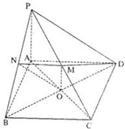
如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠ABC=60°，点M是棱PC的中点，PA⊥平面ABCD，AC、BD交于点O．
（1）已知：PA=

2

，求证：AM⊥平面PBD；
（2）若二面角M-AB-D的余弦值等于

21

7

，求PA的长．

Answer 1

（1）底面ABCD是边长为2的菱形，AC、BD交于点O．故O为AC的中点，
又∵点M是棱PC的中点，
∴AM、PO交点G是△PAC的重心，
∴AG=

2

3

AM=

2

3

×

1

2

PC=

6

3

，OG=

1

3

PO=

3

3

，AG²+OG²=1=AO²
∴AG⊥PO
又BD⊥AO，BD⊥PA，PA∩AO=A
∴BD⊥平面PAC，
又由AM?平面PAC，
∴BD⊥AM，
又由AG⊥BD，AM∩AG=A
∴AM⊥平面PBD；
（2）由MO∥PA
∴MO⊥平面ABCD，
过O作AB的垂线，垂足为N，则ON=

1

2

BO=

3

2

连接MN，则MN⊥AB，
∴∠MNO即为二面角M-AB-D的平面角
则

3 2

OM2+( 3 2 )2

=

21

7

，解得OM-1
PA=2OM=2