题目内容
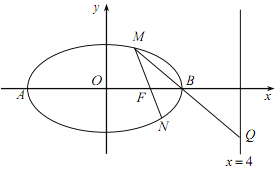
【题目】已知两点A(-![]() ,0),B(
,0),B(![]() ,0),动点P在y轴上的投影是Q,且
,0),动点P在y轴上的投影是Q,且![]() .
.
(1)求动点P的轨迹C的方程;
(2)过F(1,0)作互相垂直的两条直线交轨迹C于点G,H,M,N,且E1,E2分别是GH,MN的中点.求证:直线E1E2恒过定点.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)设出动点坐标,根据![]() 计算可得轨迹C的方程.(2)分两种情况考虑,当两直线的斜率都存在且不为0时,分别设出两直线的方程,联立方程组求得
计算可得轨迹C的方程.(2)分两种情况考虑,当两直线的斜率都存在且不为0时,分别设出两直线的方程,联立方程组求得![]() 、
、![]() 的中点
的中点![]() 的坐标,从而得到直线
的坐标,从而得到直线![]() 的方程,再讨论直线所过的定点为
的方程,再讨论直线所过的定点为![]() ;当两直线的斜率分别为0和不存在时,直线
;当两直线的斜率分别为0和不存在时,直线![]() 的方程为y=0,也过点
的方程为y=0,也过点![]() ,从而可得结论成立.
,从而可得结论成立.
试题解析:
(1)解:设点P坐标为(x,y),
∴点Q坐标为(0,y).
∵2![]() ·
·![]() =|
=|![]() |2,
|2,
∴2[(-![]() -x)(
-x)(![]() -x)+y2]=x2,
-x)+y2]=x2,
化简得点P的轨迹方程为![]() +
+![]() =1.
=1.
(2)证明:①当两直线的斜率都存在且不为0时,
设直线![]() 的方程为y=k(x-1),则直线
的方程为y=k(x-1),则直线![]() 的方程为y=
的方程为y=![]() (x-1).
(x-1).
由 消去y整理得(2k2+1)x2-4k2x+2k2-4=0.
消去y整理得(2k2+1)x2-4k2x+2k2-4=0.
则Δ>0恒成立.
设G(x1,y1),H(x2,y2),
则x1+x2=![]() ,且x1x2=
,且x1x2=![]() .
.
∴GH中点E1坐标为![]() ,
,
同理,MN中点E2坐标为![]() ,
,
∴ ,
,
∴直线![]() 的方程为
的方程为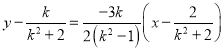 ,
,
整理得y=![]()
![]() ,
,
∴直线![]() 过定点
过定点![]() .
.
②当两直线的斜率分别为0和不存在时,直线![]() 的方程为y=0,也过点
的方程为y=0,也过点![]() .
.
综上所述直线![]() 过定点
过定点![]() .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|