题目内容
【题目】甲、乙两人参加某种选拔测试.规定每人必须从备选的6道题中随机抽出3道题进行测试,在备选的6道题中,甲答对其中每道题的概率都是
,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.
(1)求乙得分的分布列和数学期望;
(2)规定:每个人至少得20分才能通过测试,求甲、乙两人中至少有一人通过测试的概率.
【答案】（1）
；（2）
.
【解析】
（1）设乙的得分为
的可能值有
，分别计算概率，列出分布列，求解数学期望；
（2）先由（1）中分布列算出乙通过的概率，再计算出甲通过的概率，然后计算出甲乙都没有通过的概率，用1去减即可得出甲、乙两人中至少有一人通过测试的概率.
（1）设乙的得分为的可能值有
乙得分的分布列为:
X | 0 | 10 | 20 | 30 |
P |
|
|
|
|
所以乙得分的数学期望为
(2) 乙通过测试的概率为
甲通过测试的概率为
,
甲、乙都没通过测试的概率为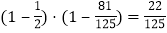
所以甲、乙两人中至少有一人通过测试的概率为
阅读快车系列答案
【题目】某大学高等数学这学期分别用
两种不同的数学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分和优秀率都相同；勤奋程度和自觉性都一样）.现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图。 学校规定：成绩不得低于85分的为优秀
（1）根据以上数据填写下列的
的列联表
甲 | 乙 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
（2）是否有
的把握认为成绩优异与教学方式有关？”(计算保留三位有效数字)
下面临界值表仅供参考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数
（份）与收入
（元）之间有如下的对应数据：
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：①参考公式：线性回归方程系数公式
， 
；
②参考数据： 
， 
， 
．
