题目内容
18.边长为2的正方形ABCD,对角线的交点为E,则($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AE}$=6.分析 由题意画出图形,求得$|\overrightarrow{AC}|=2\sqrt{2},|\overrightarrow{AE}|=\sqrt{2}$,然后展开数量积公式得答案.
解答 解:如图,
∵正方形ABCD的边长为2,∴$|\overrightarrow{AC}|=2\sqrt{2},|\overrightarrow{AE}|=\sqrt{2}$,
则($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{AE}$=$\overrightarrow{AB}•\overrightarrow{AE}+\overrightarrow{AC}•\overrightarrow{AE}$=$2\sqrt{2}cos45°+2\sqrt{2}×\sqrt{2}$=$2\sqrt{2}×\frac{\sqrt{2}}{2}+4=6$.
故答案为:6.
点评 本题考查了平面向量的数量积运算,是基础的计算题.

练习册系列答案
相关题目
9.下列函数中,周期为π,且在$[\frac{π}{4},\frac{π}{2}]$上为减函数的是( )
| A. | $y=cos(x+\frac{5π}{2})$ | B. | $y=cos(2x+\frac{5π}{2})$ | C. | $y=sin(x+\frac{5π}{2})$ | D. | $y=sin(2x+\frac{5π}{2})$ |
13.已知(1+x)n(n∈N*)的展开式中第3项与第8项的二项式系数相等,则这两项的二项式系数为( )
| A. | 36 | B. | 45 | C. | 55 | D. | 120 |
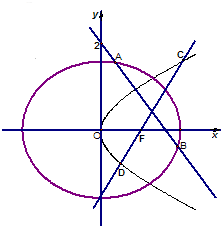 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同. 如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1.
如图,在多面体ABCDEF中,FA⊥平面ABCD,BA⊥AD,FE∥AD∥BC,M为CE的中点,EF=FA=AB=BC=$\frac{1}{2}$AD=1. 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.