题目内容
17.已知函数f(x)=xetx-ex+1,其中t∈R,e=2.71828…是自然对数的底数.(Ⅰ)当t=0时,求函数f(x)的最大值;
(Ⅱ)证明:当t<1-$\frac{1}{e}$时,方程f(x)=1无实数根;
(Ⅲ)若函数f(x)是(0,+∞)内的减函数,求实数t的取值范围.
分析 (Ⅰ)当t=0时,求导数,确定函数的单调性,即可求函数f(x)的最大值;
(Ⅱ)先确定原方程无负实数根,令g(x)=$\frac{lnx}{x}$,求出函数的值域,方程f(x)=1无实数根,等价于1-t∉(-∞,$\frac{1}{e}$],即可证明结论;
(Ⅲ)利用函数f(x)是(0,+∞)内的减函数,确定t<1,再分类讨论,即可求实数t的取值范围.
解答 (Ⅰ)解:当t=0时,f(x)=x-ex+1,
∴f′(x)=1-ex,
∴x<0,f′(x)>0;x>0,f′(x)<0,
∴函数f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,
∴函数f(x)的最大值为f(0)=0;
(Ⅱ)证明:由f(x)=1,可得x=ex(1-t)>0,
∴原方程无负实数根,
故有$\frac{lnx}{x}$=1-t.
令g(x)=$\frac{lnx}{x}$,则g′(x)=$\frac{1-lnx}{{x}^{2}}$,
∴0<x<e,g′(x)>0;x>e,f′(x)<0,
∴函数g(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
∴函数g(x)的最大值为g(e)=$\frac{1}{e}$,
∴函数g(x)的值域为(-∞,$\frac{1}{e}$];
方程f(x)=1无实数根,等价于1-t∉(-∞,$\frac{1}{e}$],
∴1-t>$\frac{1}{e}$,
∴t<1-$\frac{1}{e}$,
∴当t<1-$\frac{1}{e}$时,方程f(x)=1无实数根;
(Ⅲ)解:f′(x)=etx[1+tx-e(1-t)x]
由题设,x>0,f′(x)≤0,
不妨取x=1,则f′(1)=et(1+t-e1-t)≤0,
t≥1时,e1-t≤1,1+t≤2,不成立,∴t<1.
①t≤$\frac{1}{2}$,x>0时,f′(x)=etx[1+tx-e(1-t)x]≤${e}^{\frac{x}{2}}$(1+$\frac{x}{2}$-${e}^{\frac{x}{2}}$),
由(Ⅰ)知,x-ex+1<0,∴1+$\frac{x}{2}$-${e}^{\frac{x}{2}}$<0,∴f′(x)<0,
∴函数f(x)是(0,+∞)内的减函数;
②$\frac{1}{2}$<t<1,$\frac{t}{1-t}$>1,∴$\frac{1}{1-t}$ln$\frac{t}{1-t}$>0,
令h(x)=1+tx-e(1-t)x,则h(0)=0,h′(x)=(1-t)[$\frac{t}{1-t}$-e(1-t)x]
0<x<$\frac{1}{1-t}$ln$\frac{t}{1-t}$,h′(x)>0,
∴h(x)在(0,$\frac{1}{1-t}$ln$\frac{t}{1-t}$)上单调递增,
∴h(x)>h(0)=0,此时,f′(x)>0,
∴f(x)在(0,$\frac{1}{1-t}$ln$\frac{t}{1-t}$)上单调递增,有f(x)>f(0)=0与题设矛盾,
综上,当且仅当t≤$\frac{1}{2}$时,函数f(x)是(0,+∞)内的减函数.
点评 本题考查导数知识的综合运用,考查函数的单调性与最值,考查学生分析解决问题的能力,难度大.

 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 15$\sqrt{2}$米 | B. | 15$\sqrt{3}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 15$\sqrt{6}$米 |
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
| A. | $y=cos(x+\frac{5π}{2})$ | B. | $y=cos(2x+\frac{5π}{2})$ | C. | $y=sin(x+\frac{5π}{2})$ | D. | $y=sin(2x+\frac{5π}{2})$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同. 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
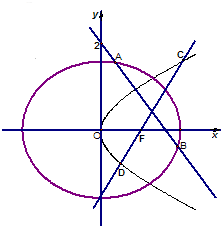
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1. 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.