题目内容
3.已知函数f(x)=ex,g(x)=x+a,a∈R.(1)若曲线f(x)=ex与g(x)=x+a相切,求实数a的值;
(2)记h(x)=f(x)g(x),求h(x)在[0,1]上的最小值;
(3)当a=0时,试比较ef(x-2)与g(x)的大小.
分析 (1)研究函数的切线主要是利用切点作为突破口求解;
(2)通过讨论函数在定义域内的单调性确定最值,要注意对字母m的讨论;
(3)比较两个函数的大小主要是转化为判断两个函数的差函数的符号,然后转化为研究差函数的单调性研究其最值.
解答 解:(1)设曲线f(x)=ex与g(x)=x+a相切于点P(x0,y0),由f′(x)=ex,知${e}^{{x}_{0}}$=1解得x0=0.
又可求得P为(0,1),所以代入g(x)=x+a,解得a=1.
(2)因为h(x)=(x+a)ex,所以h′(x)=ex+(x+a)ex=(x-(-a-1))ex,x∈[0,1].
①当-a-1≤0,即a≥-1时,h′(x)≥0,此时h(x)在[0,1]上单调递增,所以h(x)max=h(1)=(1-m)e;
②当0<-a-1<1,即-2<a<-1时,当x∈(0,-a-1)时,h′(x)<0,h(x)单调递减,
当x∈(-a-1,1)时,h′(x)>0,h(x)单调递增,h(0)=a,h(1)=(1+a)e.
(i)当a≥(1+a)e,即-2<a≤$\frac{e}{e-1}$时,h(x)max=h(0)=a.
(ii)当a<(1+a)e,即-$\frac{e}{e-1}$<a<-1时,h(x)max=h(1)=(1+a)e.
③当-a-1≥1,即a≤2时,h′(x)≤0,此时h(x)在[0,1]上单调递减,所以h(x)max=h(0)=a.
综上,当a>-$\frac{e}{e-1}$时,h(x)max=(1+a)e;当a≤-$\frac{e}{e-1}$时,h(x)max=a.
(3)当a=0时,ef(x-2)=${e}^{{e}^{x-2}}$,g(x)=x.
①当x≤0时,显然ef(x-2)>g(x);
②当x>0时,lnef(x-2)=ex-2.lng(x)=lnx.
记函数ω(x)=ex-2-lnx,则ω′(x)=ex-2-$\frac{1}{x}$,可知ω′(x)在(0,+∞)上递增,
又由ω′(1)<0,ω′(2)>0知:ω′(x)=0在(0,+∞)上有唯一实根x0,且1<x0<2,
则ω′(x0)=0,即${e}^{{x}_{0}-2}$=$\frac{1}{{x}_{0}}$(*),
当x∈(0,x0)时ω′(x)<0,ω(x)递减;当x∈(x0,+∞)时,ω′(x)>0,ω(x)单调递增.
所以ω(x)≥ω(x0),结合(*)式,知x0-2=-lnx0,
所以ω(x)≥ω(x0)=$\frac{1}{{x}_{0}}$+x0-2=$\frac{({x}_{0}-1)^{2}}{{x}_{0}}$>0,
则ω(x)=ex-2-lnx>0,即ex-2>lnx,所以${e}^{{e}^{x-2}}$>x,
综上ef(x-2)>g(x).
点评 本题综合考查了利用导数研究函数的单调性、最值基本思路,当比较两个函数大小的时候,就转化为两个函数的差的单调性,进一步确定最值确定符号比较大小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
| A. | -5 | B. | 1 | C. | 7 | D. | 2 |
| A. | 36 | B. | 45 | C. | 55 | D. | 120 |

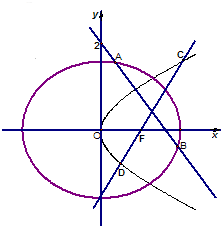 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.