题目内容
16．若x，y满足约束条件$\left\{\begin{array}{l}2x-y-4≤0\\ x-y+1≥0\\ x≥4\end{array}\right.$，则目标函数z=x+2y的最小值为12．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程在求出最优解的坐标，代入目标函数得答案．
解答 由约束条件$\left\{\begin{array}{l}2x-y-4≤0\\ x-y+1≥0\\ x≥4\end{array}\right.$作出可行域如图，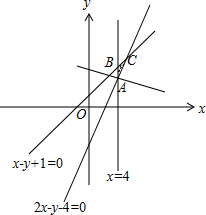
联立$\left\{\begin{array}{l}{x=4}\\{2x-y-4=0}\end{array}\right.$，解得A（4，4），
化目标函数z=x+2y为$y=-\frac{1}{2}x+\frac{z}{2}$，由图可知，当直线过A（4，4）时，
直线在y轴上的截距最小，z有最小值为4+2×4=12．
故答案为：12．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
6．在长方体ABCD-A1B1C1D1中，AB=$\sqrt{2}{，_{\;}}_{\;}BC=A{A_1}$=1，点P为对角线AC1上的动点，点Q为底面ABCD上的动点（点P，Q可以重合），则B1P+PQ的最小值为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3}{2}$ | D． | 2 |
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示
11．若i为虚数单位，则复数$\frac{i}{{\sqrt{3}-i}}$等于（ ）
| A． | $-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | B． | $\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | C． | $-\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | D． | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ |
8．已知等差数列{an}满足a6+a10=20，则下列选项错误的是（ ）
| A． | S15=150 | B． | a8=10 | C． | a16=20 | D． | a4+a12=20 |
5．
一汽车厂生产A，B，C三类轿车，某月的产量如下表（单位：辆）：
按分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆．
（Ⅰ）求a的值；
（Ⅱ）用分层抽样的方法在A，B类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆A类轿车的概率；
（Ⅲ）用随机抽样的方法从A，B两类轿车中各抽取4辆，进行综合指标评分，经检测它们的得分如图，比较哪类轿车综合评分比较稳定．
一汽车厂生产A，B，C三类轿车，某月的产量如下表（单位：辆）：| 类别 | A | B | C |
| 数量 | 400 | 600 | a |
（Ⅰ）求a的值；
（Ⅱ）用分层抽样的方法在A，B类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆A类轿车的概率；
（Ⅲ）用随机抽样的方法从A，B两类轿车中各抽取4辆，进行综合指标评分，经检测它们的得分如图，比较哪类轿车综合评分比较稳定．