题目内容
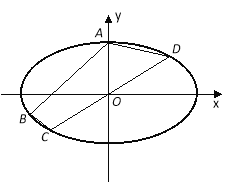
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】【试题分析】(Ⅰ)先建立动直线的方程,再运用消参法探求轨迹方程; (Ⅱ)借助直线与椭圆的位置关系推证:
(Ⅰ)依题意知直线A1N1的方程为![]() ①
①
直线A2N2的方程为![]() ②………………………………2分
②………………………………2分
设M(x,y)是直线A1N1与A2N2交点,①×②得 ![]() ,
,
由mn=2,整理得![]() ; ………………………………4分
; ………………………………4分
(Ⅱ)设![]() ,
,![]()
由 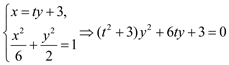 (
(![]() ) ………………………………6分
) ………………………………6分
由![]() 故
故![]() , ………………8分
, ………………8分
要证![]() ,即证
,即证![]() ,只需证:
,只需证:![]()
只需![]() 即证
即证 ![]() 即
即![]() ,………10分
,………10分
由(![]() )得:
)得:![]() ,即证. ……………………12分
,即证. ……………………12分
(本题亦可先证直线NQ过焦点F,再由![]() 得证)
得证)

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目