题目内容
20.已知函数f(x)=(x-1)(x-2)(x-3)…(x-2008),求f′(1).分析 构造函数设g(x)=(x-2)(x-3)…(x-2008),则f(x)=(x-1)g(x),再根据导数的运算法则求导,带值计算即可.
解答 解:设g(x)=(x-2)(x-3)…(x-2008),
∴g(1)=(1-2)(1-3)…(1-2008)=-1×2×3×…×2007=-2007!
则f(x)=(x-1)g(x),
∴f′(x)=g(x)+(x-1)g′(x),
∴f′(1)=g(1)+(1-1)g′(1)=g(1)=-2007!.
点评 本题考查了导数的运算法则,关键是构造函数,属于基础题.

练习册系列答案
相关题目
8.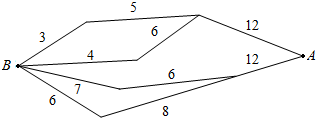 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
10.“条件甲:$\frac{1}{4}≤{2^a}≤\frac{1}{2}$”是“条件乙:(a+1)(a+2)≤1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |