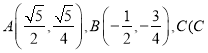题目内容
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
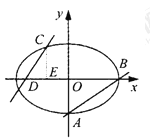
(1)求椭圆的方程.
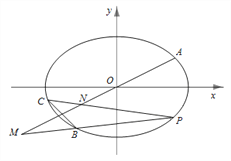
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
【答案】(1)![]() ;(2)存在
;(2)存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.
【解析】
试题分析:(1)由![]() 两点的坐标可得直线
两点的坐标可得直线![]() 方程,根据点到线的距离公式可得
方程,根据点到线的距离公式可得![]() 间的关系式,再结合离心率及
间的关系式,再结合离心率及![]() 可解得
可解得![]() 的值.(2)将直线方程与椭圆方程联立消去
的值.(2)将直线方程与椭圆方程联立消去![]() 整理为关于
整理为关于![]() 的一元二次方程.根据有2个交点可知其判别式大于0得
的一元二次方程.根据有2个交点可知其判别式大于0得![]() 的范围.由上式可得两根之和,两根之积.以
的范围.由上式可得两根之和,两根之积.以![]() 为直径的圆过点
为直径的圆过点![]() 时
时![]() ,根据直线垂直斜率相乘等于
,根据直线垂直斜率相乘等于![]() 可得
可得![]() 的值.若满足前边判别式大于0得的
的值.若满足前边判别式大于0得的![]() 的范围说明存在,否则说明不存在.
的范围说明存在,否则说明不存在.
试题解析:解:解析:(1)直线![]() 方程为:
方程为:![]() .
.
依题意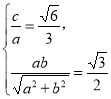 解得
解得 
∴ 椭圆方程为![]() .
.
(2)假若存在这样的![]() 值,由
值,由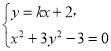 得
得![]()
![]() .
.
∴ ![]() ①
①
设![]() ,
,![]() 、
、![]() ,
,![]() ,则
,则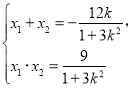 ②
②
而![]() .
.
要使以![]() 为直径的圆过点
为直径的圆过点![]() ,当且仅当
,当且仅当![]() 时,则
时,则![]() ,即
,即![]()
∴![]() ③
③
将②式代入③整理解得![]() .经验证,
.经验证,![]() ,使①成立.
,使①成立.
综上可知,存在![]() ,使得以
,使得以![]() 为直径的圆过点
为直径的圆过点![]() .
.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.