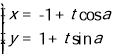题目内容
【题目】设集合A![]() ,集合B
,集合B![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围___________.
的取值范围___________.
【答案】![]()
【解析】∵对任意m∈R,都有2m≤2m+1,所以B≠,
集合B表示在直线x+y=2m与直线x+y=2m+1之间的平面区域(包含边界).
当![]() >m2,即0<m<
>m2,即0<m<![]() 时,A=,不满足条件;
时,A=,不满足条件;
当![]() ≤m2,即m≤0或m≥
≤m2,即m≤0或m≥![]() 时,A≠.
时,A≠.
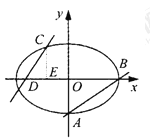
(1)若m≤0,则A={(x,y)|(x﹣2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
半径为|m|的圆面(m=0时是(2,0)),
A∩B≠等价于点(2,0)到直线x+y=2m+1的距离不大于半径|m|,
即![]() ≤|m|,即2m2﹣4m+1≤0,即(m﹣1)2≤
≤|m|,即2m2﹣4m+1≤0,即(m﹣1)2≤![]() ,解得1﹣
,解得1﹣![]() ≤m≤1+
≤m≤1+![]() ,所以m∈;
,所以m∈;
(2)若m≥![]() ,则A={(x,y)|
,则A={(x,y)|![]() ≤(x﹣2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
≤(x﹣2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
大圆半径为|m|,小圆半径为![]() 的圆环.
的圆环.
当(2,0)∈B,即2m≤2≤2m+1,即![]() ≤m≤1时,A∩B≠,满足条件;
≤m≤1时,A∩B≠,满足条件;
若m>1,则A∩B≠等价于点(2,0)到直线x+y=2m的距离不大于半径|m|,
即![]() ≤|m|,即m2﹣4m+2≤0,即(m﹣2)2≤2,解得2﹣
≤|m|,即m2﹣4m+2≤0,即(m﹣2)2≤2,解得2﹣![]() ≤m≤2+
≤m≤2+![]() ,所以1<m≤2+
,所以1<m≤2+![]() ,满足条件.
,满足条件.
综上,实数m的取值范围是[![]() ,2+
,2+![]() ].
].

【题目】天气预报是气象专家根据预测的气象资料和专家们的实际经验,经过分析推断得到的,在现实的生产生活中有着重要的意义.某快餐企业的营销部门经过对数据分析发现,企业经营情况与降雨天数和降雨量的大小有关.
(Ⅰ)天气预报说,在今后的四天中,每一天降雨的概率均为![]() ,求四天中至少有两天降雨的概率;
,求四天中至少有两天降雨的概率;
(Ⅱ)经过数据分析,一天内降雨量的大小![]() (单位:毫米)与其出售的快餐份数
(单位:毫米)与其出售的快餐份数![]() 成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
降雨量(毫米) | 1 | 2 | 3 | 4 | 5 |
快餐数(份) | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的回归方程,为尽量满足顾客要求又不造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
的回归方程,为尽量满足顾客要求又不造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
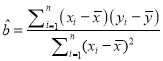 ,
, ![]()
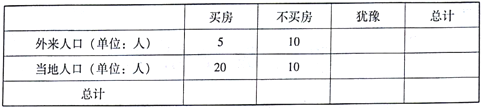
【题目】2016年5月20日,针对部分“二线城市”房价上涨过快,媒体认为国务院常务会议可能再次确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了![]() 人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
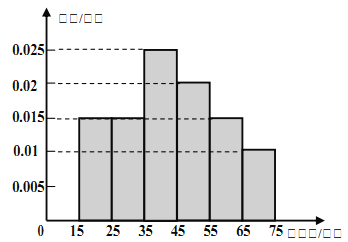
月收入(百元) | 赞成人数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)试根据频率分布直方图估计这![]() 人的中位数和平均月收入;
人的中位数和平均月收入;
(2)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人进行追踪调查,求被选取的
人进行追踪调查,求被选取的![]() 人都不赞成的概率.
人都不赞成的概率.
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中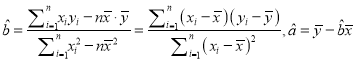 .
.