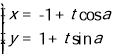题目内容
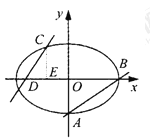
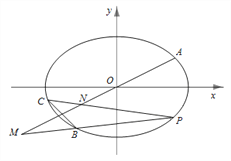
【题目】如图,已知椭圆![]() 经过不同的三点
经过不同的三点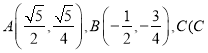 在第三象限),线段
在第三象限),线段![]() 的中点在直线
的中点在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设点![]() 是椭圆
是椭圆![]() 上的动点(异于点
上的动点(异于点![]() 且直线
且直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,问
两点,问![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)点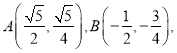 的坐标代入椭圆的方程就可求得方程,设点
的坐标代入椭圆的方程就可求得方程,设点![]() 的坐标,根据条件可得点
的坐标,根据条件可得点![]() 的坐标代入椭圆方程,BC中点坐标代入直线
的坐标代入椭圆方程,BC中点坐标代入直线![]() 的方程,两方程联立可求点
的方程,两方程联立可求点![]() 的坐标;(2)设
的坐标;(2)设![]() ,根据
,根据![]() 三点共线,用点P的坐标
三点共线,用点P的坐标![]() 表示
表示![]() ,同理用点P的坐标
,同理用点P的坐标![]() 表示
表示![]() 。再求
。再求![]() 为定值,所以
为定值,所以![]() 。
。
试题解析:(Ⅰ)由点![]() 在椭圆
在椭圆![]() 上,得
上,得 解得
解得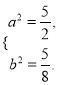 所以椭圆
所以椭圆![]() 的方程为
的方程为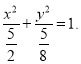 ………………………3分
………………………3分
由已知,求得直线![]() 的方程为
的方程为![]() 从而
从而![]() (1)
(1)
又点![]() 在椭圆
在椭圆![]() 上,故
上,故![]() (2)
(2)
由(1)(2)解得![]() (舍去)或
(舍去)或![]() 从而
从而![]()
所以点![]() 的坐标为
的坐标为![]() ………………………………………6分
………………………………………6分
(Ⅱ)设![]()
因![]() 三点共线,故
三点共线,故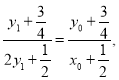 整理得
整理得![]()
因![]() 三点共线,故
三点共线,故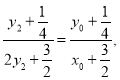 整理得
整理得![]() ……………10分
……………10分
因点![]() 在椭圆
在椭圆![]() 上,故
上,故![]() ,即
,即![]()
从而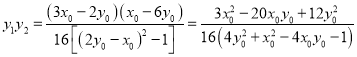
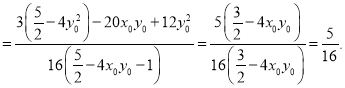
所以![]() 为定值. ………………………15分
为定值. ………………………15分

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 3 | 0 |
(1)请将上表空格中的数据在答卷的相应位置上,并求函数f(x)的解析式;
(2)若y=f(x)的图象上所有点向左平移 ![]() 个单位后对应的函数为g(x),求当x∈[﹣
个单位后对应的函数为g(x),求当x∈[﹣ ![]() ,
, ![]() ]时,函数y=g(x)的值域.
]时,函数y=g(x)的值域.