题目内容
【题目】在三棱柱![]() 中,侧面
中,侧面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 与
与![]() 交于点
交于点![]() ,
, ![]() 侧面
侧面![]() .
.
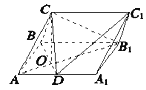
(1)证明: ![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明过程详见解析;(2)![]() .
.
【解析】试题分析:
(1)利用题意首先证得: ![]() 平面
平面![]() ,结合线面垂直的定义有:
,结合线面垂直的定义有: ![]() .
.
(2)建立空间直角坐标系,由空间坐标系求解直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
试题解析:
证明:(1)由题意可知,在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
又因为![]() ,
, ![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
又![]() 侧面
侧面![]() ,且
,且![]() 侧面
侧面![]() ,∴
,∴![]() ,
,
又![]() 与
与![]() 交于点
交于点![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
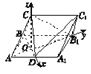
解:(2)如图所示,以![]() 为原点,分别以
为原点,分别以![]() ,
, ![]() ,
, ![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则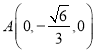 ,
, 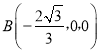 ,
, 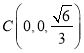 ,
, 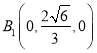 ,
, 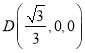 .
.
又因为![]() ,所以
,所以 ,
,
所以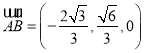 ,
, 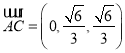 ,
, 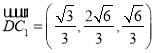 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由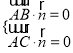 ,得
,得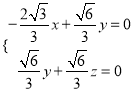 ,
,
令![]() ,则
,则![]() ,
, ![]() ,
, ![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则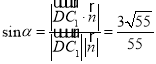 ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据
房屋面积(平方米) | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出散点图
(2)求线性回归方程
(3)根据(2)的结果估计房屋面积为150平方米时的销售价格.