题目内容
设正项数列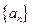 的前项和为
的前项和为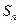 ,且
,且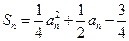 ,
,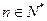 .
.
(1)求数列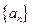 的通项公式;
的通项公式;
(2)是否存在等比数列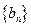 ,使
,使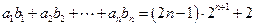 对一切正整数都成立?并证明你的结论.
对一切正整数都成立?并证明你的结论.
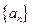 的前项和为
的前项和为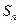 ,且
,且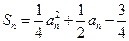 ,
,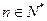 .
.(1)求数列
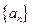 的通项公式;
的通项公式; (2)是否存在等比数列
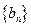 ,使
,使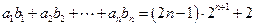 对一切正整数都成立?并证明你的结论.
对一切正整数都成立?并证明你的结论.(1)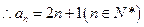
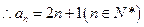
(1)由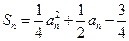 得:
得: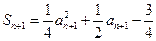 ,
,
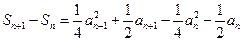
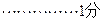
相减并整理得: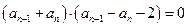
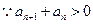 ,
,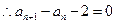 ,即
,即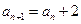
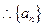 是等差数列
是等差数列
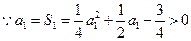 ,
,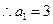
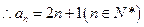
(2)由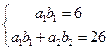 ,解得:
,解得: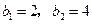
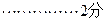
猜想: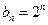 ,使
,使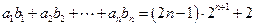 成立
成立
下面证明猜想成立:即证 对一切正整数都成立
对一切正整数都成立
令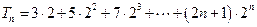 ,
,
则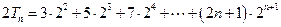
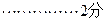
两式相减得: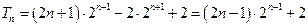
故原命题获证 .
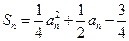 得:
得: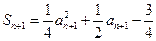 ,
,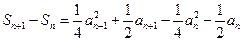
相减并整理得:
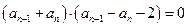
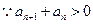 ,
,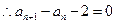 ,即
,即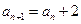
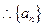 是等差数列
是等差数列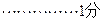
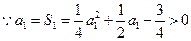 ,
,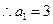
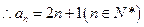
(2)由
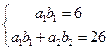 ,解得:
,解得: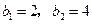
猜想:
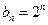 ,使
,使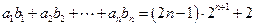 成立
成立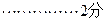
下面证明猜想成立:即证
 对一切正整数都成立
对一切正整数都成立令
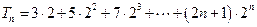 ,
,则
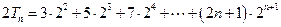
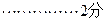
两式相减得:
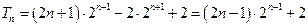
故原命题获证 .

练习册系列答案
相关题目
 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点 位于函数
位于函数 的图象上.以点
的图象上.以点 与
与 轴都相切,且⊙
轴都相切,且⊙ 又彼此外切.若
又彼此外切.若 ,且
,且
 .
. 是等差数列;
是等差数列; ,
, , 求证:
, 求证:

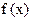 ,若存在
,若存在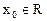 ,使
,使 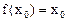 成立,则称
成立,则称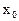 为
为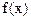 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 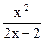 .
.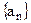 的各项均为负数,且满足
的各项均为负数,且满足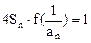 ,求数列
,求数列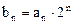 ,求
,求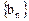 的前项和
的前项和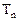 .
.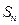 是等差数列
是等差数列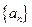 的前
的前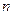 项和,且
项和,且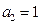 ,
,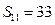 .
.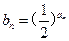 ,求证:数列
,求证:数列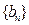 为等比数列,并求数列
为等比数列,并求数列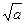 、
、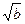 、
、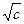 也成等差数列,则△ABC的形状为________________.
也成等差数列,则△ABC的形状为________________.
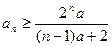 ;
;
 的前n项和
的前n项和 .
.