题目内容
对于函数 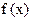 ,若存在
,若存在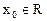 ,使
,使 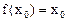 成立,则称
成立,则称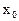 为
为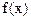 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 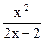 .
.
(I)试问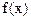 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列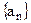 的各项均为负数,且满足
的各项均为负数,且满足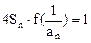 ,求数列
,求数列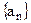 的通项公式;
的通项公式;
(III)已知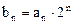 ,求
,求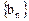 的前项和
的前项和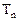 .
.
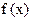 ,若存在
,若存在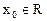 ,使
,使 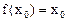 成立,则称
成立,则称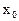 为
为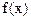 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 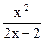 .
.(I)试问
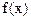 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;(II)已知数列
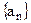 的各项均为负数,且满足
的各项均为负数,且满足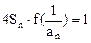 ,求数列
,求数列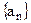 的通项公式;
的通项公式;(III)已知
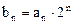 ,求
,求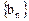 的前项和
的前项和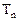 .
. (1)f(x)存在两个滞点0和2 (2)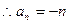
(3)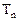 .
.
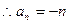
(3)
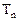 .
.
:(I)由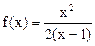 令
令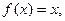
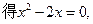 解得
解得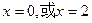
即f(x)存在两个滞点0和2
(II)由题得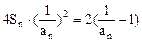 ,
,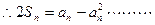 ①
①
故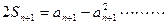 ②
②
由②-①得 ,
,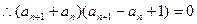
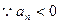
 ,即
,即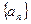 是等差数列,且
是等差数列,且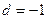
当n=1时,由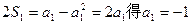
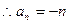
(III)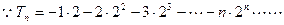 ③
③
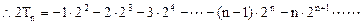 ④
④
由④-③得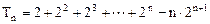

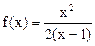 令
令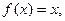
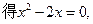 解得
解得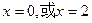
即f(x)存在两个滞点0和2
(II)由题得
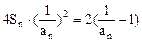 ,
,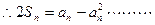 ①
①故
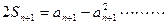 ②
②由②-①得
 ,
,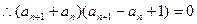
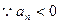
 ,即
,即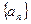 是等差数列,且
是等差数列,且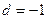
当n=1时,由
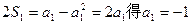
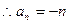
(III)
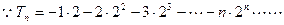 ③
③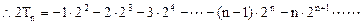 ④
④由④-③得
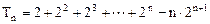


练习册系列答案
相关题目
 满足
满足 .
. 时,证明不等式:
时,证明不等式: .
. 的前
的前 项和
项和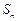 满足
满足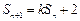 ,且
,且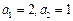

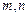 ,使
,使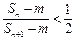 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由. 和正项等比数列
和正项等比数列 ,a7是b3和b7的等比中项.
,a7是b3和b7的等比中项. 的通项公式;
的通项公式; ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn.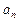 表示某企业第n年投入的治理污染的环保费用,用
表示某企业第n年投入的治理污染的环保费用,用 表示该企业第n年的产值. 设
表示该企业第n年的产值. 设 (万元)且以后治理污染的环保费用每年比上一年增加2
(万元)且以后治理污染的环保费用每年比上一年增加2 (万元);又设
(万元);又设 (万元),且企业的产值每年比上一年的平均增长率为10%. 用
(万元),且企业的产值每年比上一年的平均增长率为10%. 用 表示企业第n年 “对社会的有效贡献率”
表示企业第n年 “对社会的有效贡献率”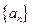 的前项和为
的前项和为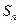 ,且
,且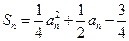 ,
,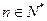 .
.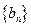 ,使
,使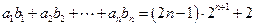 对一切正整数都成立?并证明你的结论.
对一切正整数都成立?并证明你的结论.


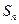


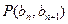
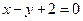
 ;
;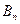 ,比较
,比较 与2的大小;
与2的大小;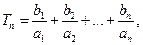 若
若 (
( ),求C的最小值
),求C的最小值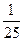 ,d>0且从第10项开始每项都大于1,则公差d的取值范围是____________________.
,d>0且从第10项开始每项都大于1,则公差d的取值范围是____________________.