题目内容
我们用部分自然数构造如下的数表:用aij(i≥j)表示第i行第j个数(i、j为正整数),使ail=aii="i" ;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第n(n为正整数)行中各数之和为bn.
(1)试写出b2一2b1;,b3-2b2,b4-2b3,b5-2b4,并推测bn+1和bn的关系(无需证明);
(2)证明数列{bn+2}是等比数列,并求数列{bn}的通项公式bn;
(3)数列{ bn}中是否存在不同的三项bp,bq,br(p,q,r为正整数)恰好成等差数列?若存在求出P,q,r的关系;若不存在,请说明理由.
(1)试写出b2一2b1;,b3-2b2,b4-2b3,b5-2b4,并推测bn+1和bn的关系(无需证明);
(2)证明数列{bn+2}是等比数列,并求数列{bn}的通项公式bn;
(3)数列{ bn}中是否存在不同的三项bp,bq,br(p,q,r为正整数)恰好成等差数列?若存在求出P,q,r的关系;若不存在,请说明理由.
 |
(1)bn+1-2 bn=2(2)bn =3×2n-1-2(3)不存在
(1)bl=1,;b2=4;b3=10;b4=22;b5=46:
可见:b2-2 bl=2;b3-2 b2=2;b4-2 b3=2;b5-2 b4=2
猜测:bn+1-2 bn="2" (或bn+1="2" bn+2或bn+1- bn=3×2n-1)
(2)由(1)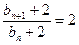
所以{bn+2},是以b1+2=3为首项,2为公比的等比数列,
∴ bn+2=3×2n-1 ,即bn =3×2n-1-2。。-
(注:若考虑, 且不讨论n=1,扣1分)
且不讨论n=1,扣1分)
(3)若数列{ bn }中存在不同的三项bp, bq, br(p,q,r∈N)恰好成等差数列,不妨设p>q>r,显然,{ bn }是递增数列,则2 bq= bp, + br
即2×(3×2q-1-2)=(3×2p-1-2)+(3×2r-1-2),于是2×2q-r=2q-r+1
由p,q,r∈N且p>q>r知,q-r≥1,p-r≥2
∴等式的左边为偶数,右边为奇数,不成立,故数列{bn}中不存在不同的三项bp,bq,br(p,q,r∈N)恰好成等差数列--
可见:b2-2 bl=2;b3-2 b2=2;b4-2 b3=2;b5-2 b4=2
猜测:bn+1-2 bn="2" (或bn+1="2" bn+2或bn+1- bn=3×2n-1)
(2)由(1)
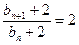
所以{bn+2},是以b1+2=3为首项,2为公比的等比数列,
∴ bn+2=3×2n-1 ,即bn =3×2n-1-2。。-
(注:若考虑,
 且不讨论n=1,扣1分)
且不讨论n=1,扣1分) (3)若数列{ bn }中存在不同的三项bp, bq, br(p,q,r∈N)恰好成等差数列,不妨设p>q>r,显然,{ bn }是递增数列,则2 bq= bp, + br
即2×(3×2q-1-2)=(3×2p-1-2)+(3×2r-1-2),于是2×2q-r=2q-r+1
由p,q,r∈N且p>q>r知,q-r≥1,p-r≥2
∴等式的左边为偶数,右边为奇数,不成立,故数列{bn}中不存在不同的三项bp,bq,br(p,q,r∈N)恰好成等差数列--

练习册系列答案
相关题目
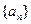 的公差
的公差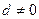 ,对任意
,对任意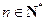 ,都有
,都有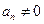 .
.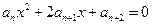 均有一个相同的实数根;
均有一个相同的实数根;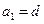 ,方程
,方程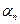 ,
,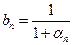 ,求数列
,求数列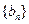 的前n项和
的前n项和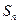 .
. 满足
满足 .
. 时,证明不等式:
时,证明不等式: .
. 和正项等比数列
和正项等比数列 ,a7是b3和b7的等比中项.
,a7是b3和b7的等比中项. 的通项公式;
的通项公式; ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn. ;(Ⅱ)求{an}前n项和Sn的最大值.
;(Ⅱ)求{an}前n项和Sn的最大值.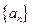 的前项和为
的前项和为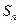 ,且
,且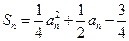 ,
,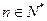 .
.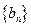 ,使
,使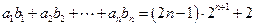 对一切正整数都成立?并证明你的结论.
对一切正整数都成立?并证明你的结论.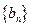 的前
的前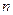 项和为
项和为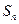 ,且
,且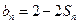 ;数列
;数列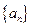 为等差数列,且
为等差数列,且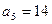 ,
,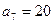 .(1)求数列
.(1)求数列 ,
,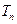 为数列
为数列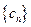 的前
的前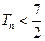 .
.