题目内容
【题目】在正方体ABCD-A1B1C1D1中,M、N分别是AB、BC的中点.

(1)求证:MN∥平面A1B1C1D1
(2)求证:平面B1MN⊥平面BB1D1D.
【答案】(1)证明见解析,(2)证明见解析
【解析】
(1)根据三角形中位线性质得![]() ,根据平行四边形性质得
,根据平行四边形性质得![]() ,即得
,即得![]() ,再根据线面平行判定定理得结果;
,再根据线面平行判定定理得结果;
(2)根据正方形性质得![]() ,即得
,即得![]() ,由正方体性质得
,由正方体性质得![]() 平面
平面![]() ,即得
,即得![]() ,再根据线面垂直判定定理得
,再根据线面垂直判定定理得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结果.
,最后根据面面垂直判定定理得结果.
(1)因为M、N分别是AB、BC的中点,所以![]() ,
,
因为正方体ABCD-A1B1C1D1,所以![]() 从而四边形
从而四边形![]() 为平行四边形,即得
为平行四边形,即得![]() ,因此
,因此![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
(2)因为正方形ABCD,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为正方体ABCD-A1B1C1D1,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,因此
,因此![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() ,
,

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
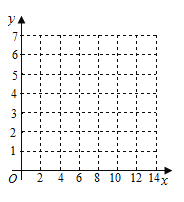
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.