题目内容
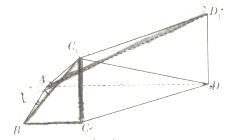
【题目】如图,直角![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() 边的中点,沿
边的中点,沿![]() 将
将![]() 折起至
折起至![]() ,且
,且![]() .
.
(1)求四棱锥![]() 的体积;
的体积;
(2)求证:平面![]() ⊥平面
⊥平面![]() .
.

【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由![]() 分别是
分别是![]() 边的中点,推出
边的中点,推出![]() 平行且等于
平行且等于![]() 的一半,则
的一半,则![]() ,即可证明
,即可证明![]() 平面
平面![]() ,从而可证平面
,从而可证平面![]() ,过
,过![]() 点作
点作![]() 于
于![]() ,可推出
,可推出![]() 平面
平面![]() ,从而可求出四棱锥
,从而可求出四棱锥![]() 的体积;(2)法一:设线段
的体积;(2)法一:设线段![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,则
,则![]() ,即可推出
,即可推出![]() 是平行四边形,再根据
是平行四边形,再根据![]() 及
及![]() ,推出
,推出![]() 是等边三角形,结合(1),可推出
是等边三角形,结合(1),可推出![]() ,从而可证平面
,从而可证平面![]() ⊥平面
⊥平面![]() ;法二:连接
;法二:连接![]() ,易证△
,易证△![]() 是边长为2等边三角形,根据
是边长为2等边三角形,根据![]() ,推出
,推出![]() ,从而推出
,从而推出![]() ,根据
,根据![]() ∥
∥![]() ,可推出
,可推出![]() ,可证
,可证![]() ,从而可证平面
,从而可证平面![]() ⊥平面
⊥平面![]() .
.
试题解析:(1)∵![]() 分别是
分别是![]() 边的中点,
边的中点,
∴![]() 平行且等于
平行且等于![]() 的一半,
的一半, ![]()
依题意, ![]() .
.
于是有 平面
平面![]() .
.
∵![]() 平面
平面![]()
∴平面![]()
过![]() 点作
点作![]() 于
于![]() ,则
,则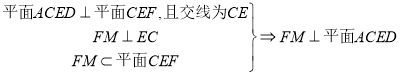 ,
,
∵![]()
∴![]()
∴梯形![]() 的面积
的面积![]()
∴四棱锥![]() 的体积
的体积![]()
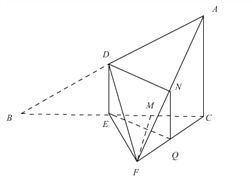
(2)(法一)如图.设线段![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,则
,则![]() ,于是
,于是 .
.
又![]() 是等边三角形.
是等边三角形.
∴EQ⊥FC
由(1)知![]() .
.
∴![]()
∴![]()
于是 .
.
∴![]()
又∵![]()
∴平面![]() ⊥平面
⊥平面![]() .
.
(法二)连接![]() ,∵
,∵![]()
∴△![]() 是边长为2等边三角形
是边长为2等边三角形
∵![]()
∴![]()
∴![]() ,
, ![]()
又∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
又∵![]() ,
,
∴![]()
又∵![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
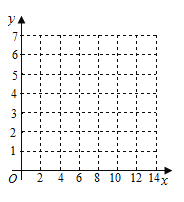
(1)请在图中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:![]() ,
,![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |