题目内容
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(I)若从袋中一次摸出2个小球,求恰为异色球的概率;
(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为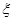 ,求
,求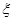 的分布列及数学期望E
的分布列及数学期望E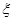 .
.
(Ⅰ) ;(Ⅱ)分布列为:
;(Ⅱ)分布列为: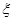
1 2 3 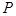
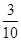
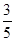
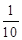
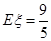 .
.
解析试题分析:(Ⅰ)若从袋中一次摸出2个小球,求恰为异色球的概率,这显然是一个古典概型,有古典概型的概率求法,先求出总的基本事件数,从8个球中摸出2个小球的种数为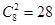 ,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为
,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为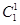
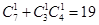 ,从而求出概率
,从而求出概率 ;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.
;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.
试题解析:(Ⅰ)摸出的2个小球为异色球的种数为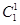
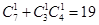 2分
2分
从8个球中摸出2个小球的种数为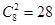 3分
3分
故所求概率为 6分
6分
(Ⅱ)符合条件的摸法包括以下三种:
一种是有1个红球,1个黑球,1个白球,
共有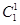
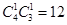 种 7分
种 7分
一种是有2个红球,1个其它颜色球,
共有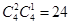 种, 8分
种, 8分
一种是所摸得的3小球均为红球,共有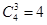 种不同摸法,
种不同摸法,
故符合条件的不同摸法共有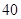 种. 10分
种. 10分
由题意知,随机变量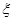 的取值为
的取值为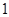 ,
,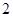 ,
,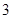 .其分布列为:
.其分布列为: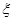
1 2 3 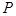
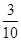
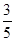
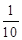
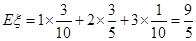 12分
12分
考点:古典概率,分布列及期望.

为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为
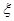 ,求随机变量
,求随机变量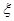 的分布列,及数学期望.
的分布列,及数学期望. 某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(Ⅲ)公司从聘用的四男
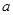 、
、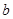 、
、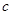 、
、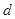 和二女
和二女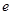 、
、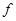 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少?  表示.
表示.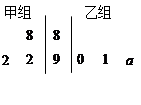
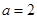 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为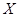 ,求随机变量
,求随机变量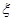 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求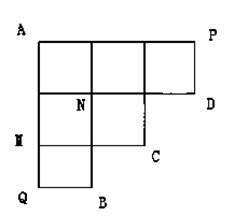
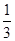 ;
;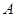 到
到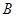 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
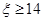 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率; 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

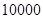 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是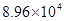 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;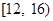 范围内的家庭中选出
范围内的家庭中选出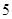 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 ,记政治、历史、地理达到优秀水平的事件分别为
,记政治、历史、地理达到优秀水平的事件分别为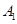 、
、 、
、 ,未达到优秀水平的事件分别为
,未达到优秀水平的事件分别为 、
、 、
、 .
. ,试求事件
,试求事件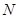 ,使得事件
,使得事件 ,并说明理由.
,并说明理由.